Notes by Lex Toumbourou

These are notes from Change of basis | Chapter 13, Essence of linear algebra by 3Blue1Brown from the Essence of linear algebra series.

If you have a vector in 2d space, the standard way to describe it is using coordinates. For example, if you have a vector $\begin{bmatrix}3 \\ 2\end{bmatrix}$, that means going from the base to 3 in the x-direction and 2 in the y-direction.

The linear algebra way to think of the coordinates is as a set of numbers that scales $\hat{i}$ and $\hat{j}$. The sum of each scaled vector is what the coordinates describe.

The first coordinate, second coordination, and unit of distance are implicit assumptions you make when describing a vector.

The choice of $\hat{i}$ and $\hat{j}$ captures all this information.

A coordinate system is a way to translate between vectors and sets of numbers.

Using a different set of basis vectors for a coordinate system is possible.

For example, a friend could have these basis vectors:

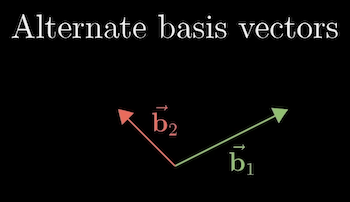
A vector $\begin{bmatrix}3 \\ 2\end{bmatrix}$ (described in the standard basis ), in your friend's basis would be $\begin{bmatrix}(5/3) \\ (1/3)\end{bmatrix}$.

Like in the standard basis, a vector in your friend's basis can be considered two coordinates that scale the basis vectors.

In our world, their basis vectors are $\vec{b}_1 = \begin{bmatrix}2 \\ 1\end{bmatrix}$ and $\vec{b}_2 = \begin{bmatrix}-1 \\ 1\end{bmatrix}$, but you should realise that in her system, those vectors are actually $\begin{bmatrix}1 \\ 0\end{bmatrix}$ and $\begin{bmatrix}0 \\ 1\end{bmatrix}$

It's akin to speaking different languages: though we are all looking at the same vectors in space, we can use other numbers to describe them.

Space has no intrinsic grid. It's simply a visual tool to follow the meaning of coordinates.

However, we all agree on the origin. Everyone agrees what coordinates $\begin{bmatrix}0 \\ 0\end{bmatrix}$ should mean.

The natural question to ask is: how do you translate between coordinate systems?

If we had vector $\begin{bmatrix}-1 \\ 2\end{bmatrix}$ in our friends basis vectors, we could translate to ours by scaling each by her basis vectors: $-1\vec{b}_1 + 2\vec{b}_2$ or $-1\begin{bmatrix}2 \\ 1\end{bmatrix} + 2\begin{bmatrix}-1 \\ 1\end{bmatrix}$.

Note that this is identical to performing Matrix-vector Multiplication: $\begin{bmatrix}2 && -1 \\ 1 && 1\end{bmatrix}\begin{bmatrix}-1 \\ 2\end{bmatrix}$, since we know that a matrix whose columns represent the basis vectors can be thought of as a transformation that moves the standard basis vectors to another set of basis vectors.

You can think of the process as first describing the vector that we "thought she meant," in other words, the vector that would express in our coordinate system, and then moving it into her coordinate system.

What about going the other way? How do you convert a vector in our basis to an alternate basis?

You start with the transformation metric for the alternate grid, then take Matrix Inverse. The inverse of a transformation takes a transform and plays it backward.

In summary, a matrix that describes an alternate coordinate system can transform from our basis into an alternate basis.

The inverse does the opposite.

---

Vectors aren't the only things we describe using coordinates. When we use a Matrix Transformation to transform a matrix, the matrix represents where our basis vectors land after the transformation.

How would we translate that matrix to another basis?

You would first convert the vector in her basis using a matrix with the alternate basis vectors to convert it to our basis.

Then, apply the transformation in our basis.

Then, apply the inverse alternate basis vectors transformation to convert back into her basis.

Since we can think of those three matrices as simply a composition of transformations, we can compose them into one transformational matrix: a transformation to the alternate basis.

When you see an expression like $A^{-1}MA$, it suggests a "mathematical sort of empathy":

• The $M$ is the transformation as "we see it."
• The outer two matrices represent the transformation as someone else sees it.