Dot Products and Duality
These are notes from Dot products and duality | Chapter 9, Essence of linear algebra) by 3Blue1Brown.
We usually teach Dot Product in an introduction to Linear Algebra course.
However, we can fully understand the Dot Product's role if we first understand Matrix Transformations.
The typical way we introduce the Dot Product is to line up components in 2 vectors with the exact dimensions and multiple the values, then add the results.
This computation has a geometric interpretation.
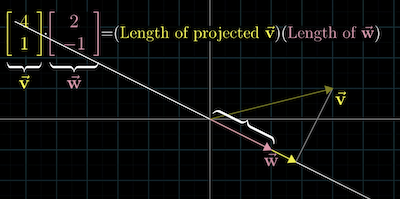
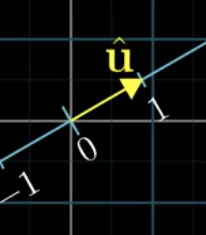
For dot product , we start by drawing a line through passing through the origin. Then, draw a line from the tip of to the first line you drew.
The dot product will equal the length of the vector from origin to the tip of the 2nd line multiplied by the length of (see cover image).
Side note for my understanding: it's helpful to understand the relationship between the dot product formula: and what 3Blue1Brown is getting at. The dot product will be 0 when the angles are perpendicular because is 0. In the visualization, has no projection onto , so we multiple by 0.
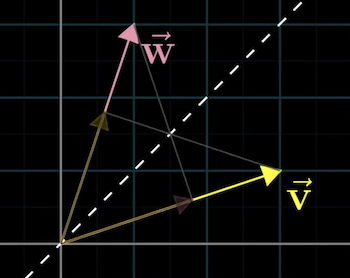
Despite how asymmetric it seems, the order doesn't matter: you can start with a line through and get the same results.
The intuition for why the order doesn't matter:
- If and were the same length, we draw a line of symmetry between them.
- Then, we project onto , it would be identical to protecting onto .
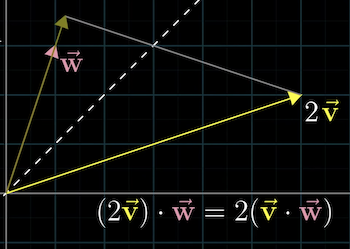
- Now, if we scaled up the vector by a factor of 2, the symmetry is broken. However, we can see that if we project onto , the length of the projection isn't changed, but the vector we're projecting on has changed.
On the other hand, if we project onto , we double the length of the projection, which has the same effect.
One question one might ask: why does the process of matching coordinates, multiplying pairs, and adding together have anything to do with projection? To understand that, we have to uncover something called duality.
But first, we need to understand linear transformations from multiple dimensions to one dimension: the number line.
Linear transformations have formal properties that make them linear:
But the video will focus on visual properties, which is equivalent to formal stuff. The intuition is that if you have a diagonal line of dots in 2d space, the dots will remain evenly spaced on the number line after a linear transformation.
Like other linear transformations, we can fully describe a linear transformation from 2d to 1d space by the landing place of the basis vectors. Where you record it to 1d space, each column is just a single number. In this example, lands on 1 and lands on -2.
Now, to follow where a vector like would land, find the vector that's and :
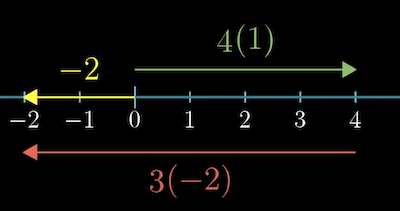
In this case, it lands on -2.
When doing the calculation numerically, it's matrix-vector multiplication. But, this is the equivalent of the dot product, but with one of the vectors tipped on the side; this suggests there's some connection between linear transformations that take vectors to numbers and vectors themselves.
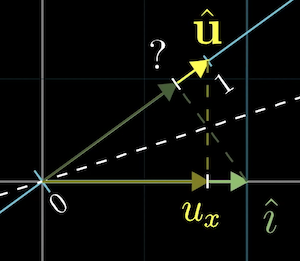
Suppose we take a copy of the number line and space it in 2d space. Then create a 2d unit vector whose tip sits on the 1 in the number line.
If you project any vector onto the number line, you have a transformation that takes 2d vectors to numbers.
The function is linear since it passes the test that lines remain evenly spaced.
Since it's a linear transformation that takes 2d vectors to numbers, you should be able to find a matrix that represents it.
The 1st element represents where lands and the 2nd where land.
To find the 2d matrix, we need to think about where and land.
Since and are unit vectors, when you project onto the line passing through , it's symmetric. So the answer is the same, asking what lands on or what lands on when projected onto the x-axis.
But, by projecting onto , it should be the same as just taking the coordinate of .
For , the reasoning is identical. The coordinate of gives you the projection onto
So the coordinates that you need are simply the coordinate of this vector on the diagonal number line .
Doing that for any vectors in space is identical to taking a dot project with , which is why taking the dot product with a unit vector can be interpreted as projecting a unit vector onto the span of some vector and taking the length.
What about non-unit vectors?
Take a non-unit vector and scale it up by 3. Numerically, each component gets multiplied by 3. So the matrix associated takes and 3x the value of where the vectors were landing before. Since it's linear, it implies that we can think of the new matrix as projecting any vector onto the number line copy and multiplying where it lands by 3. This fact explains why we can think of a dot product with a non-unit vector as first projecting onto a vector, then scaling up the length by the length of that vector.
Duality shows up in many different places in math. It refers to situations where you have a "natural-but-surprising correspondence between 2 types of mathematical thing".
In linear algebra, the "dual" of a vector is the linear transformation that it encodes. The dual of a linear transformation from 2d space to 1d is a particular vector in that space.
The most important thing to remember about the dot product is that it's a useful geometric tool for projections and testing whether vectors point in the same direction.