Notes by Lex Toumbourou

When you multiply a matrix $(A)$ by the Identity Matrix $(I)$, you get the original matrix back.

$A \cdot I = A$

It's the equivalent of multiplication with the number 1 in scalar math.

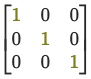
The Identity Matrix is a square: it has an equal number of rows and columns. It has the value 1 in the main diagonal from left to right and 0 everywhere else.

An identity matrix can have any number of dimensions.

In notation, we represent an Identity Matrix with $I$ and the number of dimensions $n$. For example, the Identity Matrix with three dimensions is $I_{3}$.

$I_3 = \begin{bmatrix}\color{olive}{1} & 0 & 0 \\ 0 & \color{olive}{1} & 0 \\ 0 & 0 & \color{olive}{1} \end{bmatrix}$

If we are doing Matrix Multiplication with the Identity Matrix and another square matrix, the Identity Matrix should have dimensions equal to the other matrix. The multiplication is commutive in this case: $I_n \cdot A_{(n \times n)} = A_{(n \times n)} \cdot I_n$

$\begin{bmatrix}2 & 4 \\ 1 & 3\end{bmatrix} \begin{bmatrix}\color{olive}{1} & 0 \\ 0 & \color{olive}{1}\end{bmatrix} = \begin{bmatrix}\color{olive}{1} & 0 \\ 0 & \color{olive}{1}\end{bmatrix} \begin{bmatrix}2 & 4 \\ 1 & 3\end{bmatrix}$

If the original matrix is rectangular and has dimensions $m \times n$, the size of the identity depends on which side of the expression it's on $I_m \cdot A_{(m \times n)} = A_{(m \times n)} \cdot I_n$

$\begin{bmatrix}\color{olive}{1} & 0 \\ 0 & \color{olive}{1}\end{bmatrix} \begin{bmatrix}2 & 4 & 5 \\ 1 & 3 & -2\end{bmatrix} = \begin{bmatrix}2 & 4 & 5 \\ 1 & 3 & -2\end{bmatrix} \begin{bmatrix}\color{olive}{1} & 0 & 0 \\ 0 & \color{olive}{1} & 0 \\ 0 & 0 & \color{olive}{1}\end{bmatrix}$

In this Matrix Multiplication example, we can see how the main diagonal of 1s returns the original matrix.

Multiplying a matrix by its Inverse Matrix will return the identity matrix.

When we multiply the Identity Matrix by another Identity Matrix, the result is the same matrix.

All the rows and columns in the Identity Matrix have Linear Independence.

Dye et al. (2018)

References

David Dye, Sam Cooper, and Freddie Page. Mathematics for Machine Learning: Linear Algebra - Home. 2018. URL: https://www.coursera.org/learn/linear-algebra-machine-learning/home/welcome. ↩