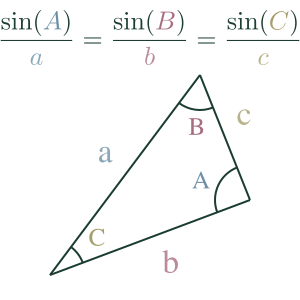Notes by Lex Toumbourou

The Law of Sines tells us that the ratio between the sine of an angle and the side opposite will be constant for any angle in a triangle.

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

If we have at least two sides and an angle or two angles and a side, we can use it to find the missing values.

Example

Question

Consider a triangle with angles $A$, $B$ and $C$ and sides $a$, $b$ and $c$, where $a$ is the side opposite $A$, $b$ opposite $B$ and $c$ opposite $C$.

If $C = 42°$, $c = 15cm$ and $b = 1cm$, solve the triangle.

Working

We can start by finding $B$ using the Law of Sines:

Since we know that $\frac{\sin 42°}{15cm} = \frac{\sin B}{1cm}$

We can calculate $\frac{\sin 42°}{15} = 0.0446$

$\frac{\sin B}{1} = 0.0446$

Since dividing by 1 equals the numerator, we know:

$\sin B = 0.0446$

Then use $\arcsin$ to find $B$

$B = arcsin(0.0446)$

$B = 2.557°$

We can now find $A$ since we know that all the angles in a triangle add up to $180°$

$A = 180° - 42° - 2.56°$

$A = 135.44°$

Now to find $a$, we can use the Law of Sines again:

$\frac{\sin 42°}{15cm} = \frac{\sin(135.44)}{a}$

Calculate the known values:

$0.0446 = 0.702 / a$

Multiply both sides by A:

$a \times 0.0446 = 0.702$

$a = \frac{0.702}{0.0446} = 15.74cm$

Now that we have the missing values, we can use the Law of Sines to check that all ratios are equal:

$\frac{sin(135.44°)}{15.74} = 0.045$

$\frac{sin(2.56°)}{1} = 0.045$

$\frac{sin(42°)}{15} = 0.045$

Answer

$A = 135.44°$

$B = 2.56°$

$C = 42°$

$a = 15.74cm$

$b = 1cm$

$c = 15cm$

See also Law Of Cosines.

---

Backlinks

• Law Of Cosines