Recursion
Recursion is a problem-solving method where a Function calls itself with a smaller instance of the problem. A Base Case is required to ensure the calls eventually terminate.
All recursive problems can be solved using iteration; however, some algorithms, particularly a Divide-and-Conquer algorithm, can be solved much more elegantly with recursion.
Fibonacci numbers example
The canonical example of a recursive solution is the Fibonacci number sequence. The sequence is the sum of the previous two numbers:
It can be expressed recursively as:
The base cases are:
We visualise a call to by representing the call stack as a tree, like this:
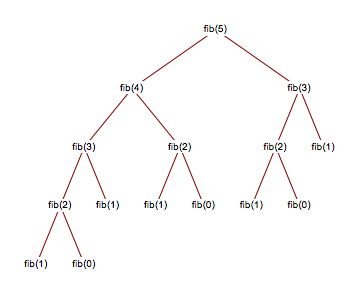
Source dhovemey at ycp (page now unavailable)
As you can see, each branch opens two new branches until we finally reach the bottom of the tree (the base case) and can finally propagate the answers back to the top.
In pseudocode:
function Fibonacci(n)
assert n >= 0
if n < 2 then
return n
end if
return Fibonacci(n-1) + Fibonacci(n-2)
end function
Factorial example
The Factorial algorithm is:
Which can be expressed recursively simply as:
The base case for Factorial comes at
We can rewrite the function in pseudocode as follows:
function Factorial(n)
if n = 0 then
return 1
end if
return n x Factorial(n - 1)
end function