Notes by Lex Toumbourou

5.201 Logic gates

• Logic Gate
  • Implementation of a boolean operation.
  • Basic element of an implementation of a Circuit.

• Basic Gates

  • Most basic logic circuits:
    • OR gates
    • AND gates
    • NOT gates
  • All Boolean functions can be written in terms of these 3 logic operations.

  • AND Gate

    • Produces HIGH output (value 1) when all inputs are HIGH otherwise, output is LOW (value 0).
    • For a 2-input gate, AND gate is represented by electrical notation and truth table:

    

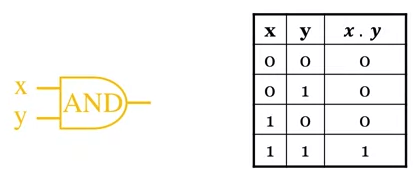
    • The AND operations is written as $f = x . y$ or $f = xy$
      • OR Gate
    • Produces HIGH output (value 1) when any of 2 inputs if HIGH, otherwise, output is LOW (value 0).
    • For a 2-input gate, OR gate is represented by electrical notation and truth table:

    

    • The OR operation is written as $f = x + y$
      • Inverter Gate
    • Produces opposite of the input.
    • Also known as NOT gate.
    • When input is LOW (0), output is HIGH (1) and vice versa.
    • The inverter gate is represented by the following electrical notation and truth table:

    

    • Not operation is written as $f = \overline{x}$
    • Other gates:
    • You can combine the basic gates to create 4 additional gates:
      • XOR Gate
    • True only when values of inputs differ

  • NAND Gate

    • AND Gate followed by an inverter.
    • Equivalent to not AND

  • NOR Gate

    • Equivalent to "not OR"
    • OR Gate followed by an inverter.

  • XNOR Gate

    • Equivalent to not XOR.
  • Multiple input gates
  • AND, OR, XOR and XNOR operations are all commutative and associative
  • They can be extended to more than 2 inputs.
  • For example:
    • The XNOR Gate can be applied to 3 inputs:
    • NAND and NOR operations are both commutative but not associative.
    • Extending number of inputs is less obvious here.
    • When writing cascaded NAND and NOR operations, must use correct parentheses.
  • Representing De Morgan's laws
  • Theorem 1
    • Complement of the product of variables, is equal to the sum of the complements of variables.
    • $\overline{x . y} = \overline{x} + \overline{y}$
  • Theorem 2
    • Complment of the sum of variables, is equal to the product of the compliment of variables
    • $\overline{x + y} = \overline{x} . \overline{y}$

5.203 Combinational circuits

• Outlines
  • Definition of a circuit
  • Building a circuit from a function
  • Writing Boolean expressions from a circuit
  • Building a circuit to model a problem
• Definition of a circuit
  • Combination Circuits (aka logic networks)
    • combination of Logic Gates designed to model Boolean functions.
    • circuit that implements a Boolean function.
    • logic values assigned to output signals is a Boolean function of current config of input signals.
• Building a circuit from a function
  • Given a Boolean function, we can implement a logic circuit representing all states of the function.
  • Want to minimise the # of gates used to minimise the cost of the circuit.
  • We can implement Boolean functions in different ways.
  • Consider Boolean function $f$:
    • $f(x, y, z) = x + y' z$
    • $f$ can be represented by this circuit:
• Writing a Boolean expression from a circuit
  • Given a logic network, we can work out its corresponding Boolean function:
    • 1. label all gate outputs that are a function of the input variables.
    • 1. express the Boolean functions for each gate in the first level.
    • 1. repeat the process until all the outputs of the circuit are written as Boolean expressions.
  • Example
    • 1. Label input of the circuit with symbols
    • 1. Express boolean functions for first level.
    • 1. Repeat for 2nd and third levels.
• Building a circuit to model a problem
  • Combinational circuits are useful for desiging systems to solve specific problems, like addition, multiplication, decoders and multiplexers.
  • Steps for building combinational circuit are:
    • 1. labelling the inputs and outsput using variables.
    • 1. modelling the problem as a Boolean expression
    • 1. replacing each operation by the equivalent logic gate.
• Building an adder circuit
  • Consider building an adder for 2 one-digit binary bits x and y.
  • From the truth table of this Boolean function, we know that:
    • $sum = xy' + x'y = x \oplus y$
    • $carry = xy$
    • 
  • Can be designed as a half adder
• Half adder has limitations:
  • no provision for carry input.
  • circuit is not useful for multi-bit additions.
• Building a full adder circuit
  • To overcome its limitations, transform half adder into a full adder by including gates for processing the carry bit.
  • sum = x $\oplus$ y $\oplus$ carry in
  • carry out = xy + carry in. (x $\oplus$ y)
  • 2 Boolean expression can be designed in as follows:
    • We can hide some of the comlexity of a circuit by using a box diagram as a simple abstraction representing just the inputs and outputs.

5.205 Simplification of circuits

• Outline
  • Benefits of simplification and Algebraic simplification
    • Show how Boolean Algebra Theorem or rules can be used to represent and simplify Boolean functions.
  • Introduce Karnaugh Map of Boolean functions.
• Benefits of simplification
  • We know that every function can be written in Sum-of-Products Form
    • Not necessarily optimal in terms of number of gates and depth of circuit.
  • Why circuits must be simplified:
    • Reduces global cost of circuits, by reducing number of logic gates used
    • Might reduce time computation cost of circuits
    • Allows more circuits to be fitted on same chip

• Algebraic simplification

  • Based on the use of Boolean algebra theorems to represent and simplify the behaviour of Boolean Functions.
  • To produce a sum-of-product expression, need to use one or all of following theorems:
    • De Morgan's laws and involution
    • Distributive laws
    • Commutative, idempotent and complement laws
    • Absorption law

  • Example

    • Consider this Boolean expression: $E = ((xy)'z)'((x'+ z)(y' + z'))'$
    • Using De Morgan's laws and involution:
      • $$

    \begin{align} E &= (xy)'' + z')((x' + =z)'+(y' + z')') \ &= (xy + z')((x'' . z') +y'' . z'') \ &= (xy + z')(xz' + yz) \end{align}

    $ * Can be further simplified using **distributive** laws: E = xyxz' + xyyz + z'xz' + z'yz$ * Using commutative, idempotent and complement laws: $E = xyz' + xyz + xz' + 0$ * Using absorption law: $E = xyz + xz'$

• Example 2

  • Consider full adder circuit from last week.
  • Using truth table, we can build a sum-of-products form for the 2 functions:
  • 
• Karnaugh Maps
  • A Karnaugh map (or K-Map) is a graphic representation of a Boolean function and differs from a truth table.
    • It can be used for expressions with 2, 3, 4 or 5 variables.
  • A K-Map is shown in an array of cells and cells differing by only one variable are adjacent.
  • The number of cells in a K-Map is the total number of possible input variable combinations which is $2^k$.
  • Example
    • Consider the Boolean function described in the truth table shown here:
      • We have 3 variables, we need a 3-input K-Map for which we identify all the 1's first.
      • Group each 1 value with the maximum possible number of adjacent 1's to form a rectangle, power of 2 long (1, 2, 4, 8)
      • Then, write a term for this rectangle.
      • In this case, it's the minimised expression of $f$ is: $x + yz$

5.211 Domino logic gates simulation

• Learn about logic gates and how to represent them using dominoes.
• Logic gates are basic element of electronic circuitts, implementing a boolean operation.
• Computers are made of billions of these tiny electrical components. Depending on characteritics of eahc gate, logic gates take information coming in and output the processed information accordingly.
• It is difficult to visualise this rpcoess in computers as the info they get is in electrical signals. The signal can either be on or off. It depends on the voltage registered.
• Can break down complex system using dominoes.
• The info is dicated by whether a chain of dominoes is falling or not, representing high voltage and low voltage respectively.
• The next exercise wil simulate different types of logic

5.208 Summative quiz

Questions I did not understand

Which of the following expressions is a sum-of-products form of the Boolean expression: $F(x, y, z) = (x+\overline{y}).z$

$F(x, y, z) = x.y.\overline{z} + x.\overline{y}.\overline{z} + x.y.\overline{z}$ $F(x, y, z) = xyz+x\overline{y}z+\overline{x}.\overline{y}$ $F(x, y, z) = \overline{x}.y.\overline{z} + x.y.z + \overline{x}.y.z$

Why is it 3 variables in each product term?

By distributivity: $F(x, y, z) = (x+\overline{y}).z = xz+\overline{y}z$ By identity: $xz+\overline{y}z=x(y+\overline{y})z+(x+\overline{x})\overline{y}z$ By distributivity: $x(y+\overline{y})z+(x+\overline{x})\overline{y}z=xyz+x\overline{y}z+x\overline{y}z+\overline{x}.\overline{y}z$ By idempotent law: $xyz+x\overline{y}z+x\overline{y}z+\overline{x}.\overline{y}z= xyz+x\overline{y}z+\overline{x}.\overline{y}z$

Find the simplification of the expression represented by the following K-map.

I accidentally got it right.

$\overline{x}+z$

Assignment

Question

Given the Boolean function $F(x, y, z) = (x + \overline{y}) . z$, write the sum-of-products expansion of $F$ where all the variables $x, y, z$ are used.

Answer

1. Distributive law: $F(x, y, z) = xz + (\neg y)z$
2. Identity law: $F(x, y, z) = x.1.z + 1.\overline{y}.z$
3. Complement law: $F(x, y, z) = x . (y + \overline{y}) . z + (x + \overline{x}) . \overline{y} . z$
4. Distributive law: $F(x, y, z) = x.y.z + x.\overline{y}.z + x.\overline{y}.z + \overline{x} .\overline{y}.z$
5. Idempotent law: $F(x, y, z) = x.y.z + x.\overline{y}.z + \overline{x} . \overline{y} . z$

Problem Sheet

1. What is the output for each of the logic circuits?

1. $\overline{A} + B$
2. $\overline{A . \overline{(B . C)}}$

How can I know the output if I don't know what the input is? Maybe some kind of algebraic reduction?

Looks like my initial answer was correct, I just didn't include the NOT part of the circuit after $B . C$

1. Write down the truth table for the output Q of the following circuit.

1. Simplify each Boolean expression to one of the following expressions: $0, 1, A, B, AB, A+B, \overline{AB}, \overline{A} + \overline{B}, \overline{A}B, A\overline{B}$
   1. $\overline{\overline{A} + \overline{B}}$
      1. $\overline{\overline{A . B}}$ -- DeMorgan's law
      2. A.B -- involution theorem
   2. $A (A + \overline{A}) + B$
      1. $(A + A.\overline{A}) + B$ -- distributivity
      2. (A + 0) + B -- complements
      3. A + B -- identity
   3. $(A + B)(\overline{A} + B)\overline{B}$
      1. $(A + B) (\overline{A} \ \overline{B} + B\overline{B})$-- Distributivity
      2. $(A + B) (\overline{A} \ \overline{B} + 0)$ -- Involution
      3. $(A + B)(\overline{A} \ \overline{B})$
      4. $(A. \overline{A} \ \overline{B} + B. \overline{A} \ \overline{B})$ -- Distributivity
      5. $(A. \overline{A} \ \overline{B} + B . \overline{B} \ \overline{A})$ -- Commutativity
      6. $(0\overline{B} + 0\overline{A})$
      7. 0 + 0
      8. 0
2. Use the laws of Boolean Algebra to simplify the boolean expression: $a + \overline{a}b = a + b$
   1. $a + \overline{a}b = a + b$
      1. $a.1 + \overline{a}b = a + b$ -- identity law
      2. $a . (1 + b) + \overline{a}b$
      3. $a1 + ab + \overline{a}b$ -- Distributive law
      4. $a.1 + b(a + \overline{a})$ -- Distributibe law
      5. $a1 + b1$ -- Complements
      6. a + b
   2. Use a truth table to prove that $a + \overline{a}b = a + b$

3. Simplified circuit is just $a + b$

1. What is the output of the following logical circuit?
   1. $p . q . r + p. \overline{q} r + p . q . \overline{r}$
   2. $p.p.p + r . r . \overline{r} + q . \overline{q} .q$
      1. $p(q + r)$
2. Use the truth table to prove De Morgan's laws:

$\overline{ab} = \overline{a} + \overline{b}$

$\overline{a + b} = \overline{a} . \overline{b}$

1. Use the laws of boolean algebra to simplify:

$\overline{ab}(\overline{a} + b)(\overline{b} + b)$

$\overline{ab}(\overline{a} + b)(1)$ -- Complement $\overline{ab}(\overline{a} + b)$ -- Idempotent $\overline{ab}\overline{a} + \overline{ab}b$ -- Distributive law

$(\overline{a} + \overline{b}) \overline{a} + (\overline{a} + \overline{b})b$ -- De Morgan's law $\overline{a}.\overline{a} + \overline{b}.\overline{a} + b\overline{a} + b\overline{b}$ -- Distributive law $\overline{a}.\overline{a} + \overline{b}.\overline{a} + b\overline{a} + 0$ -- Complement $\overline{a}.\overline{a} + \overline{b}.\overline{a} + b\overline{a} + 0$ -- Idemptotent $\overline{a} + \overline{b}.\overline{a} + b\overline{a} + 0$ -- Idemptotent $\overline{a} + \overline{a}(b + \overline{b}) + 0$ -- Distributive $\overline{a} + \overline{a}(b + \overline{b}) + 0$ -- Complement $\overline{a} + \overline{a}(1) + 0$ -- Complement $\overline{a} + \overline{a} + 0$ -- Identity $\overline{a} + \overline{a}$ -- Identity $\overline{a}$ -- Idempotent

1. Use laws of boolean algebra to simplify the boolean expression

$\overline{a}(a + b) + (b + aa)(a + \overline{b})$

$\overline{a}(a + b) + (b + a)(a + \overline{b})$ -- idempotent laws $\overline{a}(a + b) + (a + b)(a + \overline{b})$ -- commutative laws

Even the answers don't make sense here.

1. Prove that in a boolean algebra $a^2 = a$ You are required to explain your answer by making a reference to a boolean algebra axioms (laws)

a.a = a a = a -- Idempotent laws.

The answer should be:

\begin{align} a &= a.1 \\ &= a . (a + \overline{a}) \\ &= a . a + a . \overline{a} \\ &= a^2 + 0 \\ &= a^2 \\ \end{align}

1. The following diagram shows a circuit with three inputs and two outputs, $u$ and $v$

1. List the logic gates used

3 OR gates and 2 AND gates

1. Describe each output u and v as a Boolean expression in terms of x, y and z

$u = (x + y) + z$

$v = ((x + y) . z) + (x . y)$ $v = zx + zy + xy$

1. Derive the Boolean expression for the following logic circuit shown below

$((((a + b) . c) . d) . e)$

1. Write down a boolean expression for the following input/output behaviour

1. Write a boolean expression for input/output behaviour.

   $u = \overline{x}.\overline{y}.\overline{z} + \overline{x}.y.z + x.y.\overline{z}$

2. Construct the corresponding circuit of the above expression using not-games, and-gates and or-gates only