Week 14 - Graphs B
7.201 Isomorphic Graphs
-
-
Two graphs and are isomorphic if there is a bijection (invertible function) that preserves adjacency and non-adjacency.
- if is in then is in
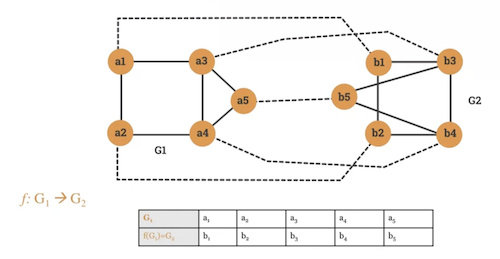
-
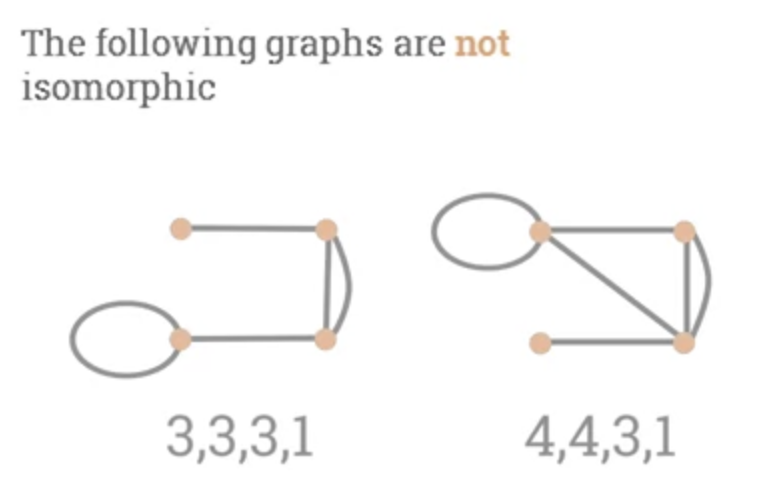
Two graphs with different degree sequences can't be ismorphic.
- Properties of isomorphic graphs
- 2 graphs with different degree sequence can't be isomorphic.
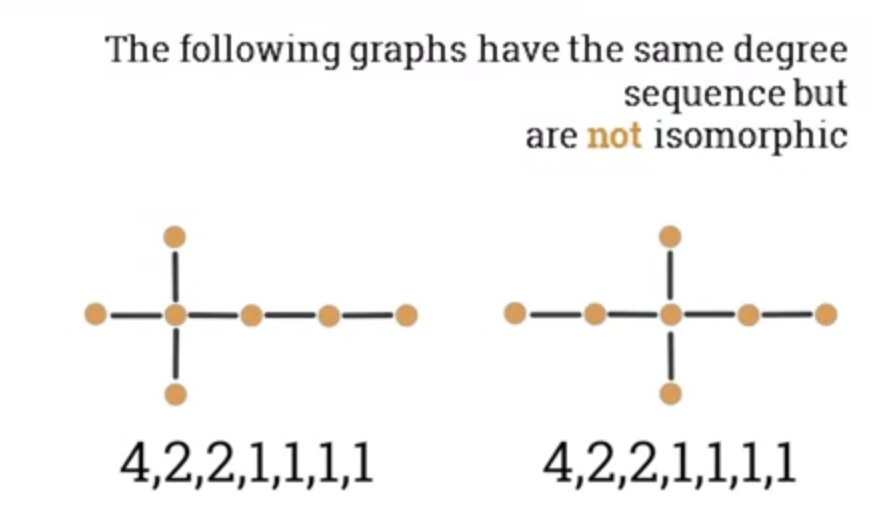
- 2 graphs with the same degree sequence may not be isomorphic.
-
7.203 Bipartite graphs
-
- A graph is called a bi-partite graph.
- If the set of vertices V can be partitioned in 2 no-empty disjoint sets and in such a way that each edge in has one endpoint in and another endpoint in .
- Example:
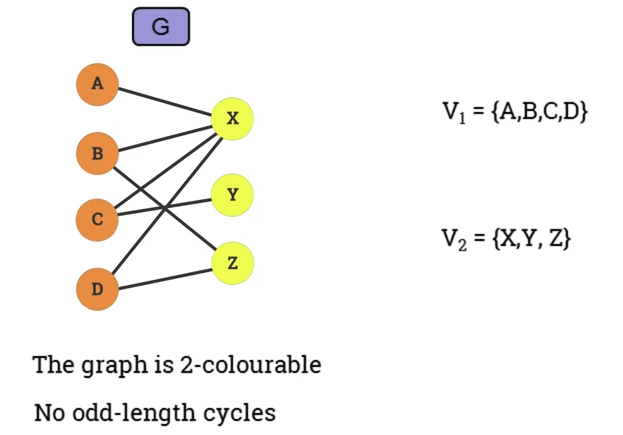
- Graph is 2-colourable.
- No odd-length cycles.
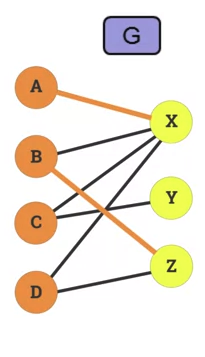
- Matching
- A set of pairwise non-adjacent edges, none of which are loops.
- ie no 2 edges share a common endpoint.
-
A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching.
- Otherwise the vertex is unmatched.
-
Maximum matching
- A maximum matching is a matching of maximum size so that if any edge is added, it's no longer matching.
- In a bitpartite graph, there can be multiple maximum matching.
-
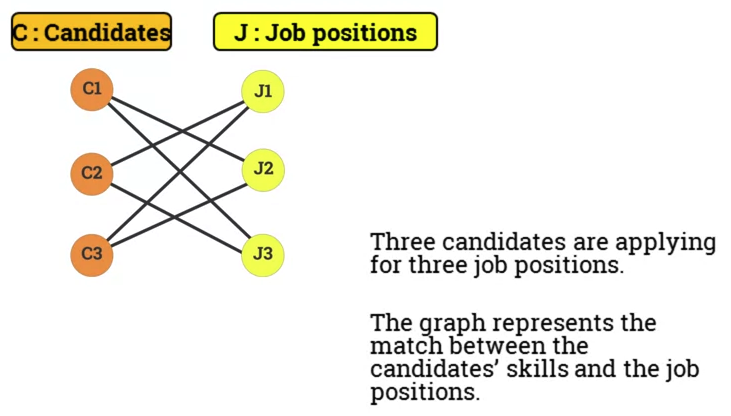
The Hopcroft-Kaft Algorithm
- An algorithm for solving the maximum matching problem in a bipartite graph.
- Concepts:
- Augmenting path: starts on a free node and alternate between unmatched unmatched edges ending on a free node
- "augments the cardinality of the current machine"
- Breadth-first search:
- Traverses the graph level by level
- Depth-first search:
- Traverses graph all the way to a leaf before starting another path.
- Augmenting path: starts on a free node and alternate between unmatched unmatched edges ending on a free node
- Example:
- Pseduo code:
- Initialise M = {}
- While there exists an Augmenting Path p
-
- Use BFS to build layers that terminate at free vertices.
-
- Start at the free vertices in C, use DFS.
-
- Return M
7.205 The adjacency matrix of a graph
-
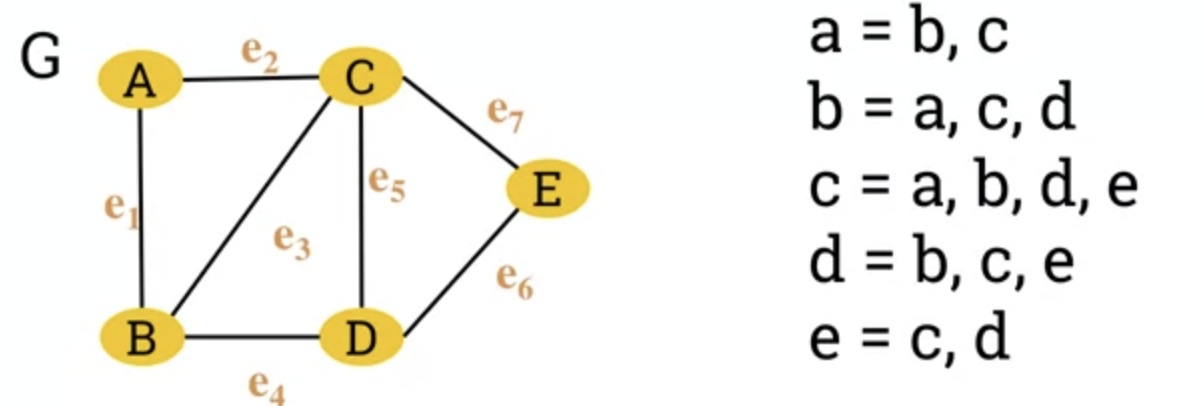
Adjaceny List of a graph.
- So far a graph has been represented by a set of vertices and a set of edges.
- Adjaceny list of a graph G is a list of all vertices in G and their corresponding individual adjacent vertices.
-
Adjacent Matrix of a graph.
- A graph can also be represented by its adjacency matrix.
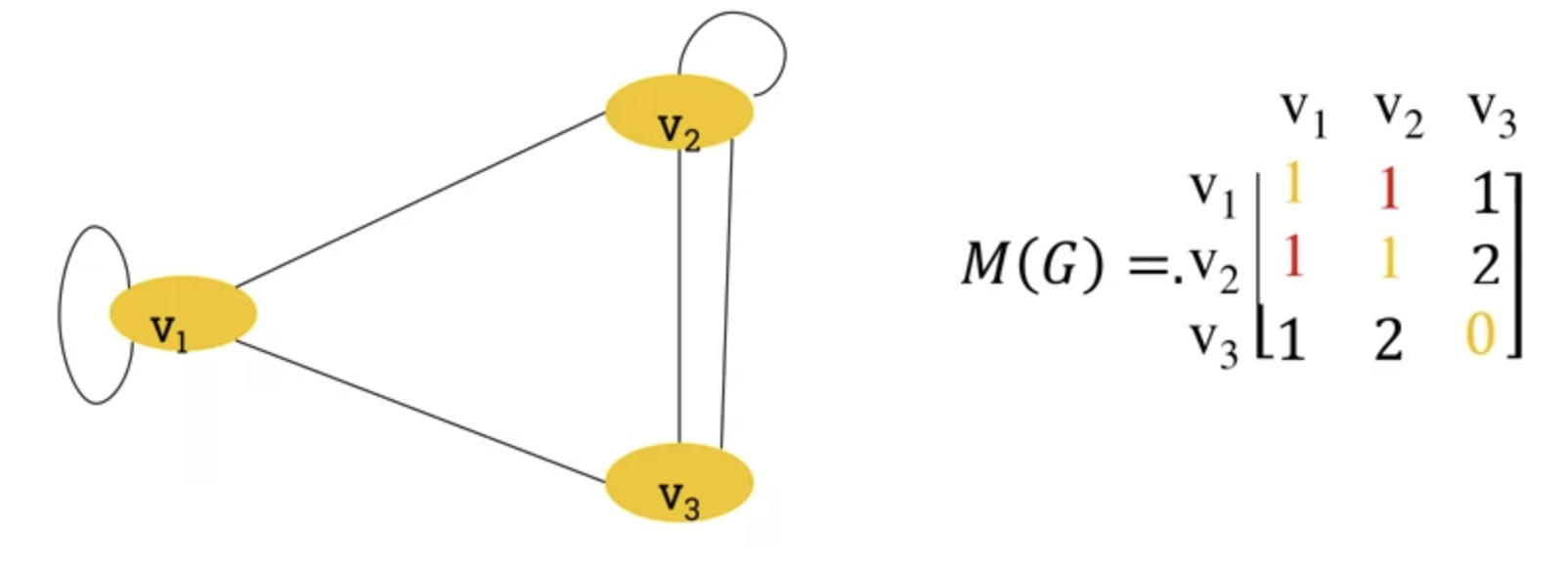
- Apparent from the loops, ever other edge is represented twice (ie v1 -> v3 and v3->v1)
- So we can multiply the diagonal by 2 to represent loops consistently.
- Properties of the adjaceny matrix.
- Adjaceny matrix of an undirected graph is symmetric.
- Number of edges in undirected graph equals half the sum of all elements ($\mathbf{m_ij}$) of its corresponding adjaceny matrix.
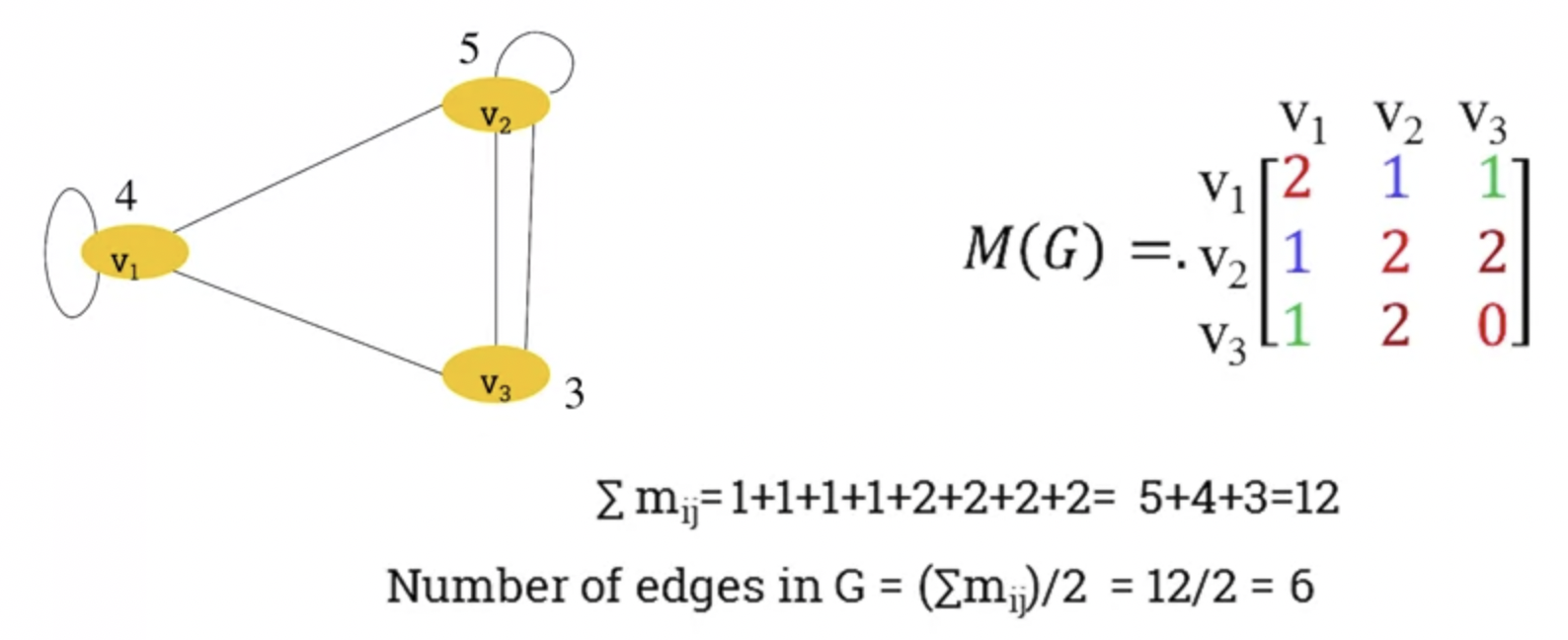
- In a directed graph, the adjaceny matrix only counts an edge pointing in a certain direction once.
7.207 Dijkstra's algorithm
-
- A weighted graph is a graph where each edge is assigned a numerical weight.
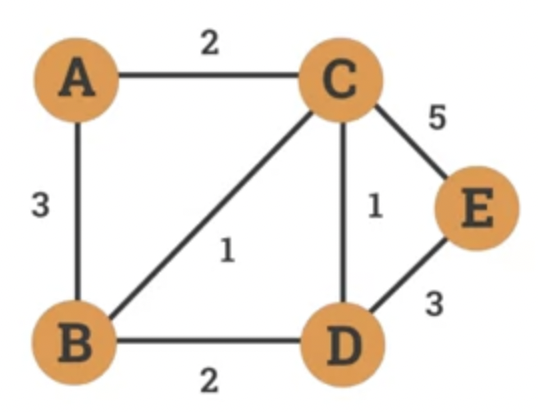
- Can be used to model:
- Distance between cities.
- Response time in communication network.
- Cost of transaction.
- Dijkstra's algorithm
- An algorithm designed by Edsger W. Dijkstra in 1956.
- Find shortest path between nodes in weighted graph.
- Example
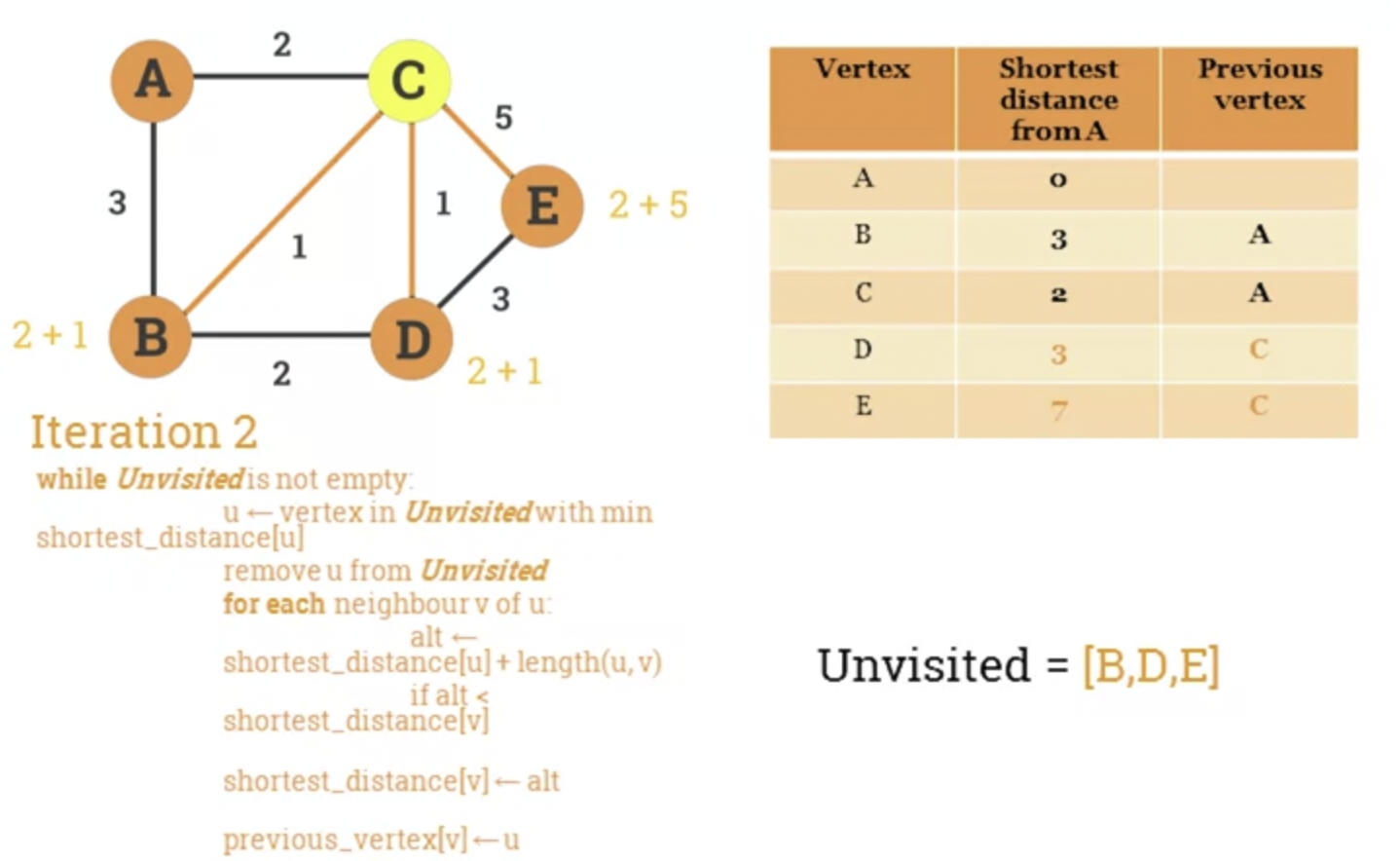
-
Algorithm's pseudocode.
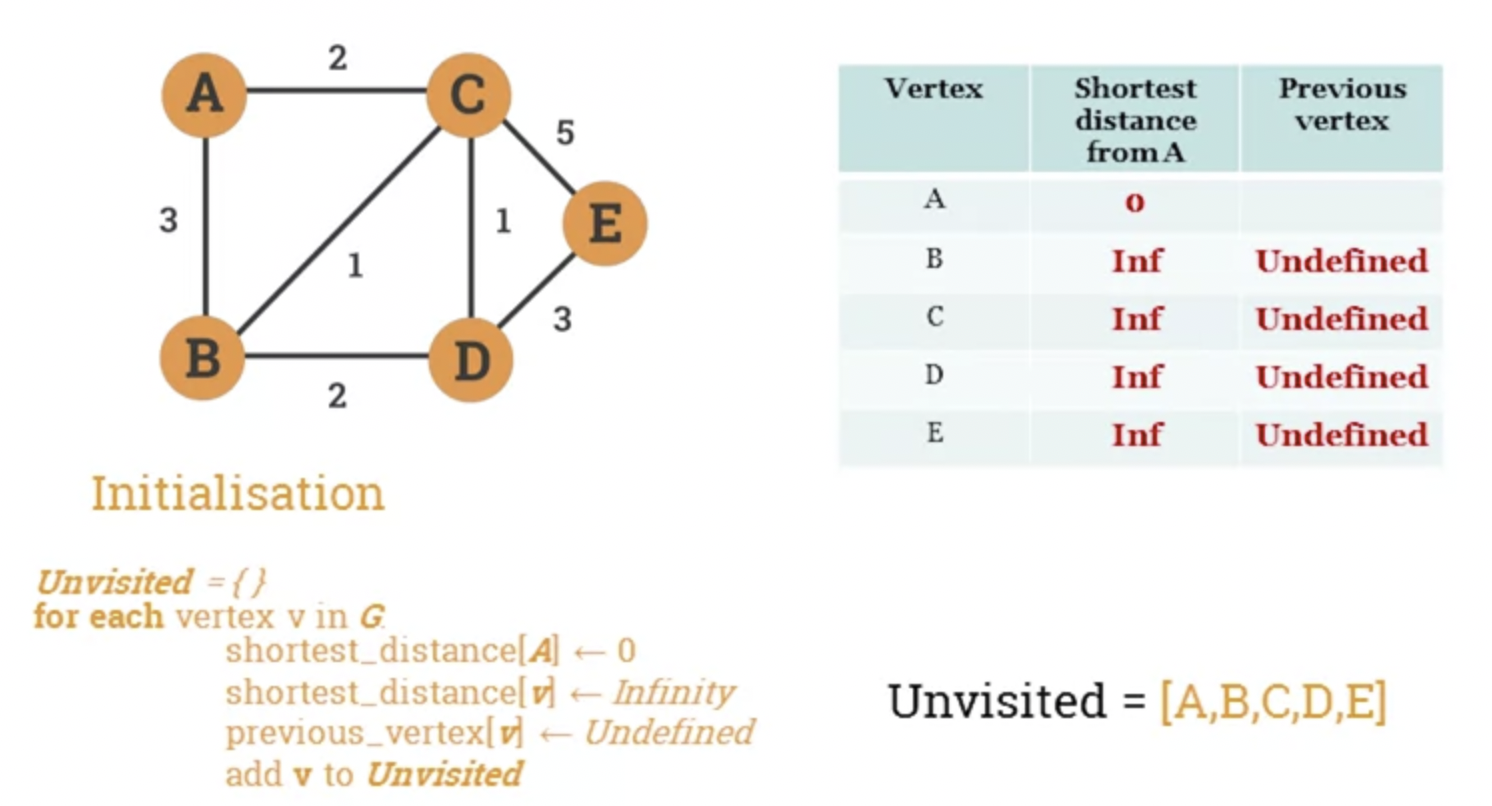
- Let G be a graph and s a source vertex.
- The following pseudocode calculates the shortest distance and previous vertex from s to every other node in the graph.
Unvisited = {}
for each vertex v in G:
shortest_distanced[v] = Infinity
previous_vertex[v] = Undefined
add v to Unvisited
shortest_distance[s] = 0
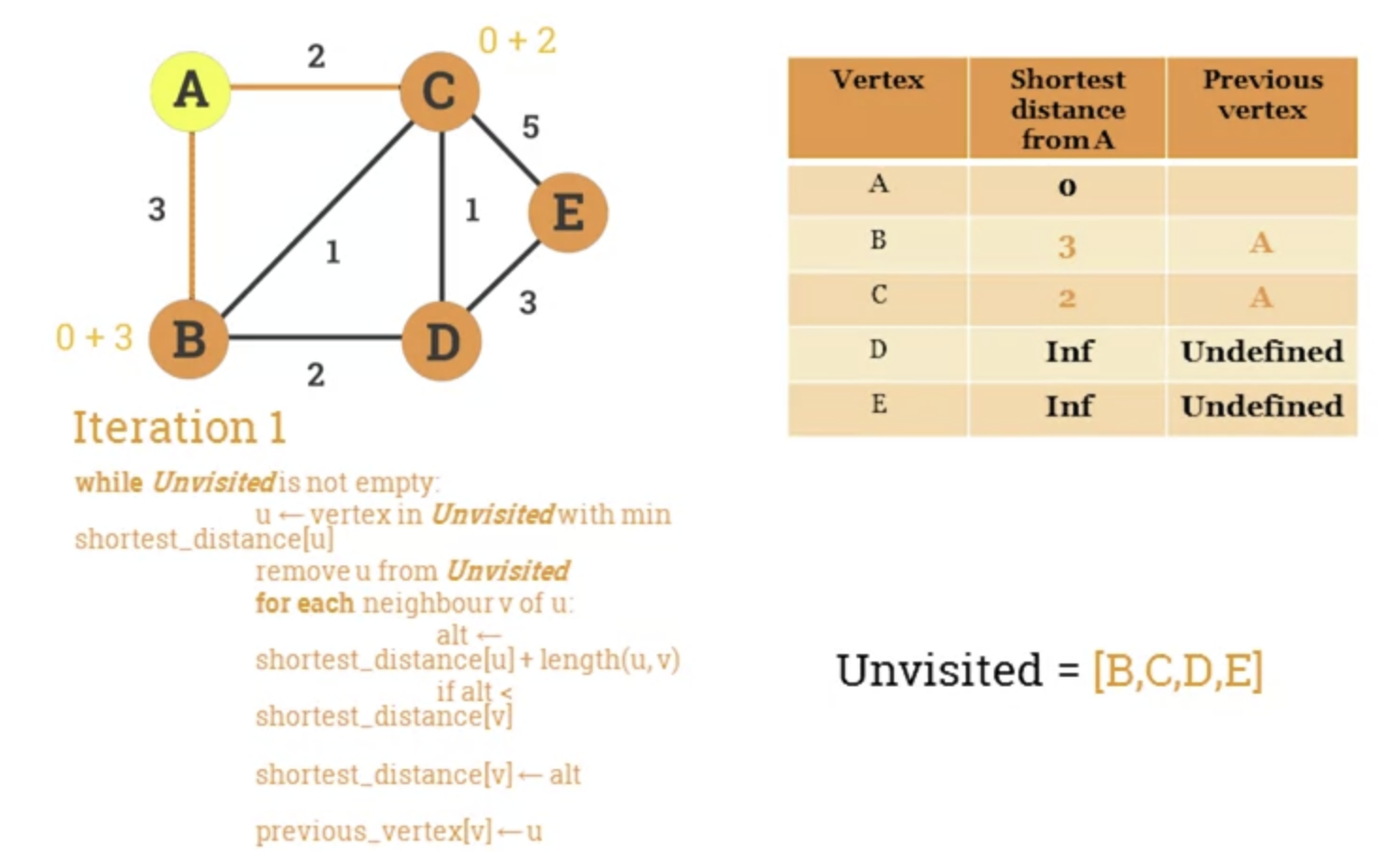
while Unvisited is not empty:
u = vertex in Unvisited with min shortest_distance[u]
remove u from Unvisited
for each neighbour v of u:
alt = shortest_distance[u] + length(u, v)
if alt < shortest_distance[v]:
shortest_distance[v] = alt
previous_vertex[v] =u
return shortest_distance, previous_vertex
Problem Sheet
Question 1
Given the following graph
- Draw the graph G
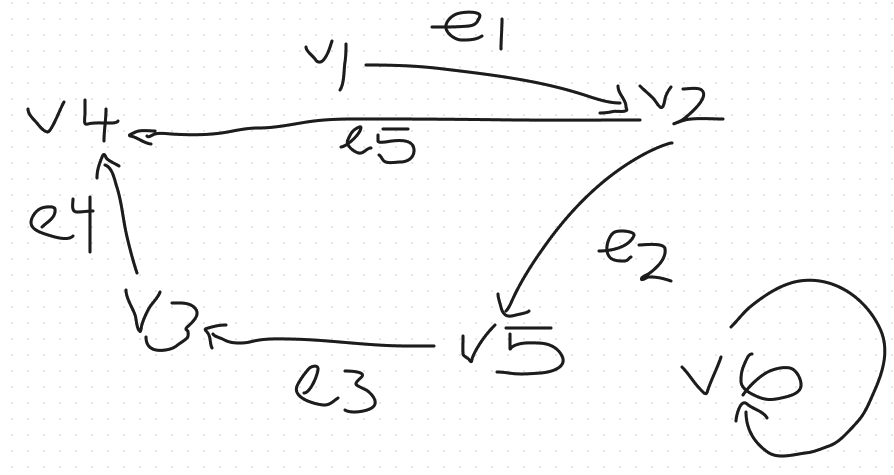
- List the set of vertices adjacent to v2
v1, v4, v5
- List the set of edges incident with v3.
(v3, v4), (v5, v3)
- Give an example of a path of length 3 starting at the vertex v2 and ending at v5.
v2, v4, v3, v5
- Give an example of a cycle length 4.
v2, v4, v3, v5, v2
Question 2
Given the following graph:
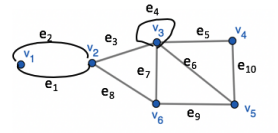
Determine which of the walks are trails, paths or circuits.
-
v1 e1 v2 e3 v3 e4 v3 e5 v4
-
Is a trail as no edge is repeated.
- Is NOT a path as v3 is repeated.
-
Is NOT a circuit as it is not closed.
-
e1 e3 e5 e5 e6
-
Is NOT a trail as e5 is repeated.
-
v2 v3 v4 v5 v3 v6 v2
v2 e3 v3 e5 v4 e10 v5 e5 v3 e7 v6 e8 v2
- Is a trail as no edge is repeated.
- Is NOT a path as v3 is repeated.
-
Is a circuit as it's a closed trail.
-
v2 v3 v4 v5 v6 v2
v2 e3 v3 e5 v4 e10 v5 e9 v6 e8 v2
- Is a trail as no edge repeated.
- Is NOT a path as v2 is repeated
-
Is a circuit from v2 to v2
-
v1 e1 v2 e1 v1
-
Not a trail as e1 is repeated.
Question 3
Which of the following undirected graphs have a Euler circuit? Which of those that do not have an Euler circuit have a Euler path?
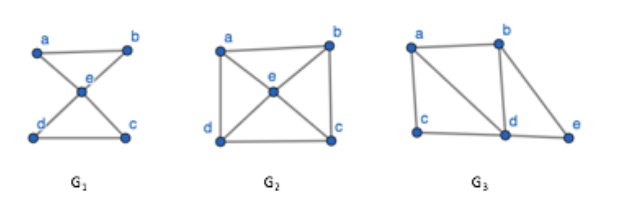
- Euler path
- A graph that has a path that uses each edge of the graph exactly once. If the path exists, the graph is considered traversable.
-
Euler Circuit
- A graph with a circuit (starts and ends on same vertice) containing all edges.
- If a graph has a Euler circuit, then every vertex of the graph has a positive even integer degree.
-
G1 has a Euler Circuit. Is has a closed trail that uses each edge exactly
ab, bd, dc, ce, ea
- G2 does not have Euler Circuit. It does not have a Euler path.
- G3 does not have a Euler Circuit. However, it does have a Euler path.
ab, bd, da, ac, cd, de, eb
Question 4
Which of the following directed graphs has an Euler circuit? Which of those that do not have a Euler path?
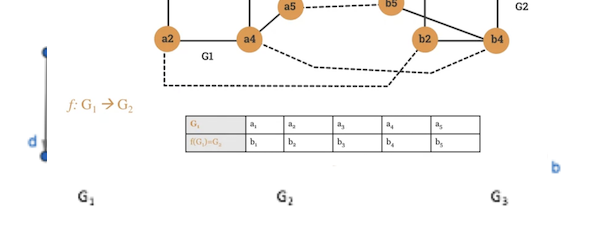
- Does not have a Euler circuit, or path.
- Does have a Euler circuit
ag, gc, cb, bg, ge, ed, df, fa
- Does not have a Euler circuit, but does have a path.
ca, ab, bc, cd, db
Question 5
In each of the following either construct a graph with the specified properties or say why it is not possible to do it.
- A graph with degree sequence 4, 3, 3, 1
The degree sequence here adds to 11. The sum of a degree sequence must be even.
- A simple graph with degree sequence 4, 3, 3, 2, 2
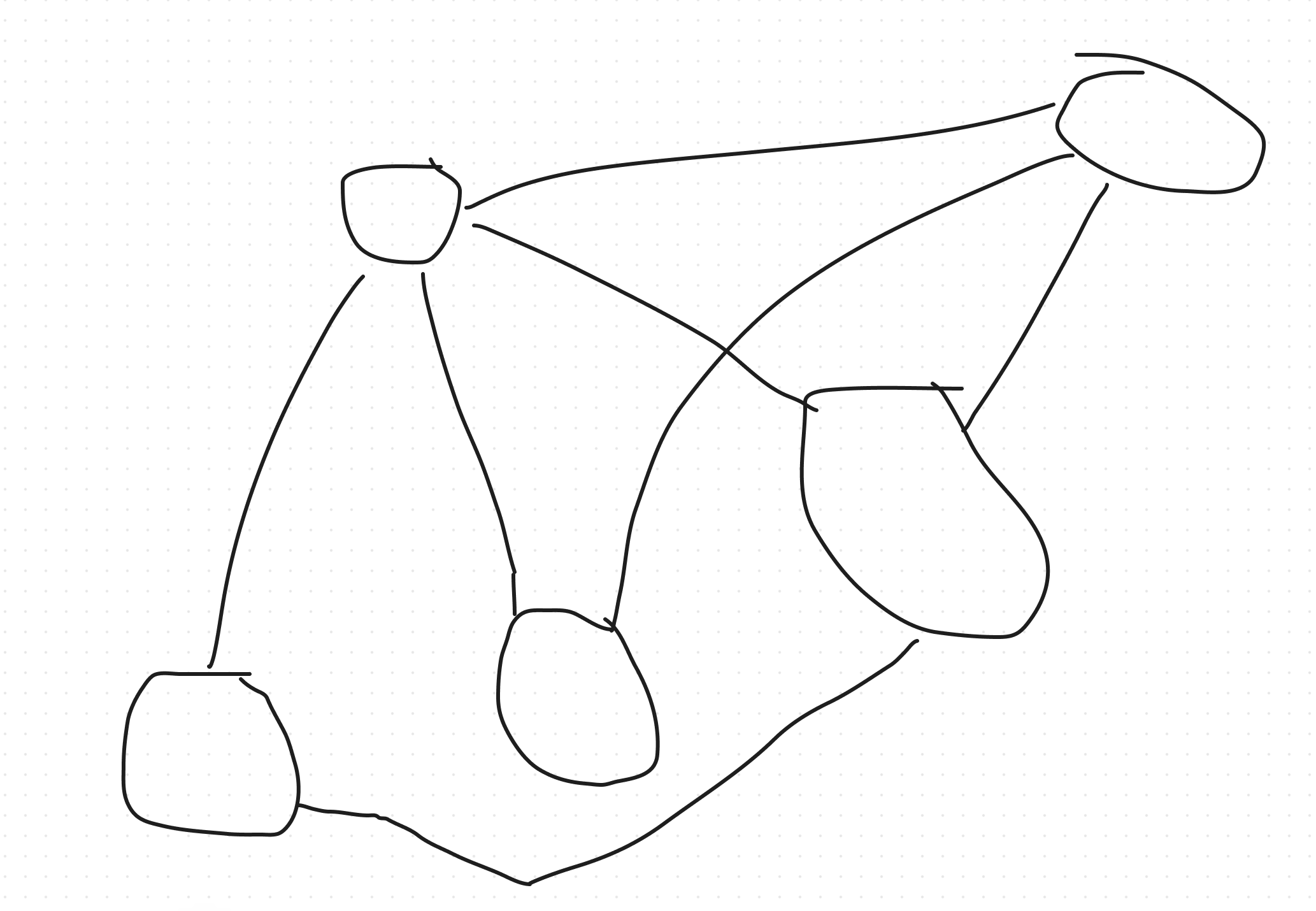
- A simple 3 regular graph with 6 vertices
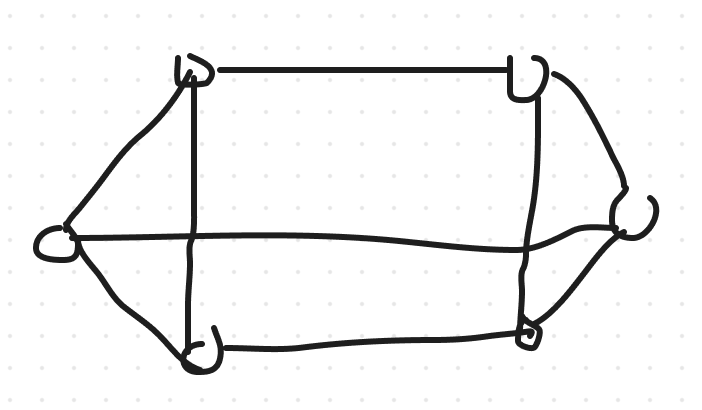 A
A
Question 6
In a group of 25 people, is it possible to each shake hands with exacty 3 other people.
I think it's not, as in order to have a degree sequence of 3 with 25 vertices, you would end up with an odd sum.
Question 7
Find a Hamiltonian circuit in the following graph:
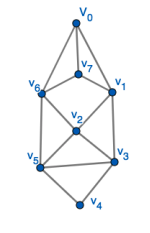

Question 8
Given the following directed graph:
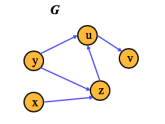
Find the transitive closure, G*, of the graph G.
To find the Transitive Closure of G, we need to add missing edges if there are any. It's constructed like this:
- Take the starting point as the graph G.
- Check if there is a directed path between and 2 vertices of G. For example, a directed path from vertex u to v.
- Then add a direct path if it's not already in the graph.
Question 9
Suppose that 7 sites are connected in a network. The number of other sites to which each site has a direct connection is given by the following sequence:
1, 2, 2, 3, 3, 4, 7
- This might describe some kind of remote office, with a head office with direct connectivity to each suboffice, then 3 countries with 1-3 sites. Each country has connectivity to other offices and head office.
- It has 7 vertices.
- The sum of degrees is twice the number of edges:
- It is impossible to construct a Simple Graph, as there are n vertices and for a simple graph, the degree of each vertices is at most n-1 or 6. We have a vertice with 7 connections.
- It is impossible to construct a network with 9 sites, with 5 connections as that would result in which is an odd number. A degree sequence must be even.
Question 10
- What is a Complete Graph?
A graph where each vertice is adjacent (linked with an edge)
- What is the degree of each vertex of the complete graph ? Calculate the number of edges in . Draw
Degree of each vertex = n - 1 = 7 Number of edges = 8 * 7 / 2 = 28
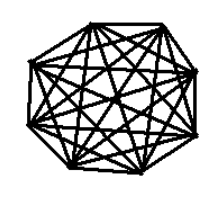
- The degree of each vertex of complete graph K_n = n -1. It will have n(n-1) / 2 edges.
Question 11
Construct 3 non isomorphic graphs with 5 vertices and 5 edges. Give one property for each graph that neither of the others has, which makes it non-isomorphic.