Week 16 - Trees B
8.201 Rooted trees
-
Rooted Trees
-
A rooted tree is a directed tree with a distinguished vertex $r4, called a root. Such that, for every vertex v there is a directed path from r to v.
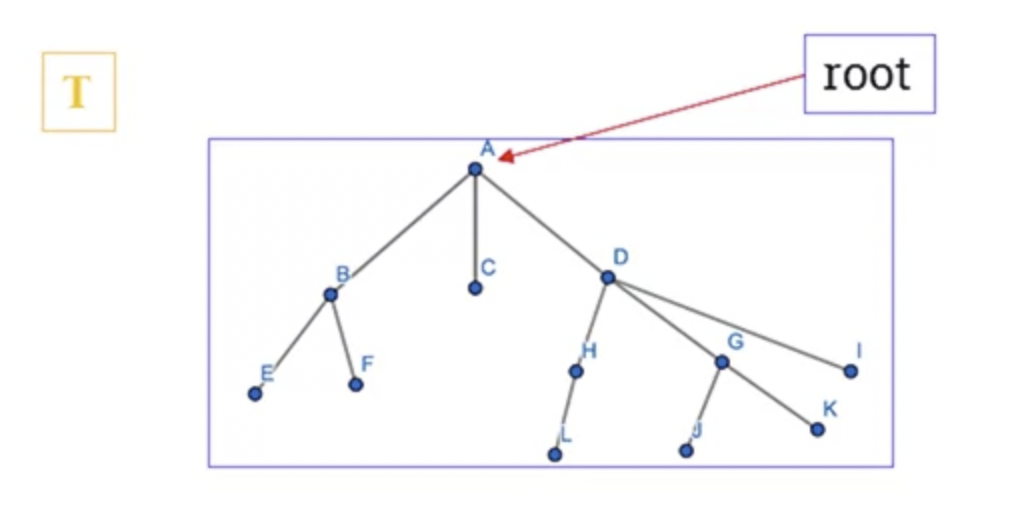
-
A directed tree is represented as a rooted tree if and only if one vertex has in-degree 0 whereas all other vertices have in-degree 1.
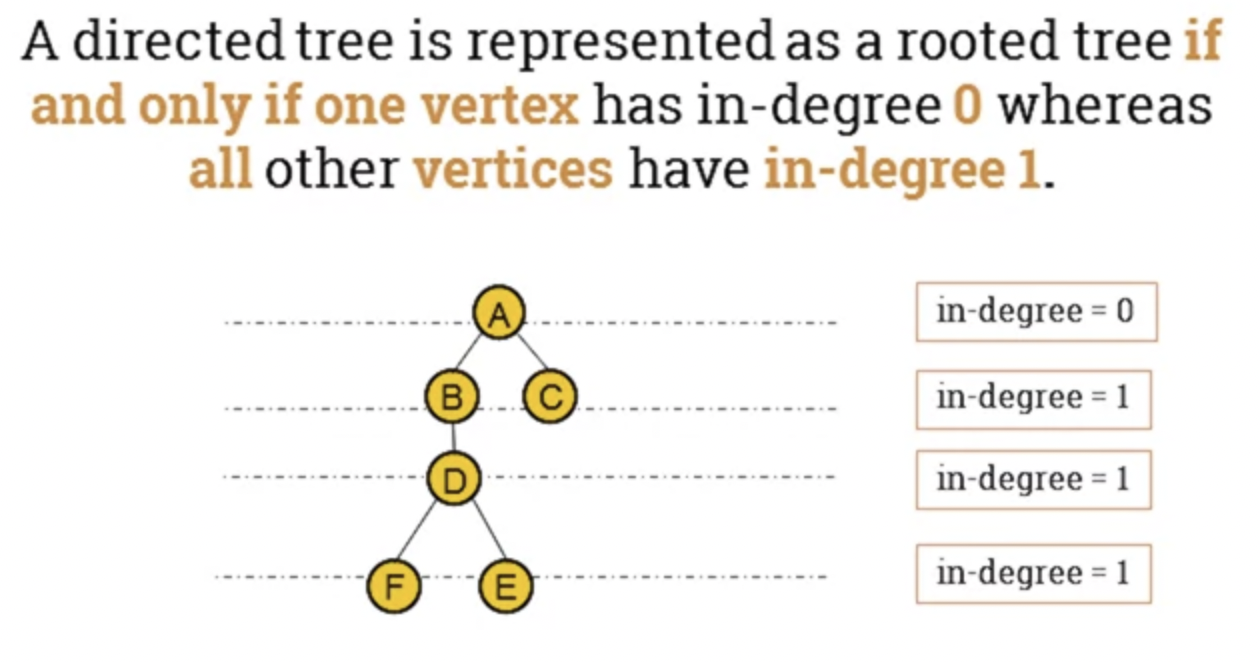
- Terminology of rooted trees.
- In the image above:
- A is the root of the tree.
- B is called the parent of D.
- E and F are the children of D.
- B and A are ancestors of E and F (E and F are siblings)
- B and D are called internal nodes.
- C, E and F are called external nodes.
- Depth and height in a tree
- Depth or path length of a node in a tree is the number of edges from root to that node.
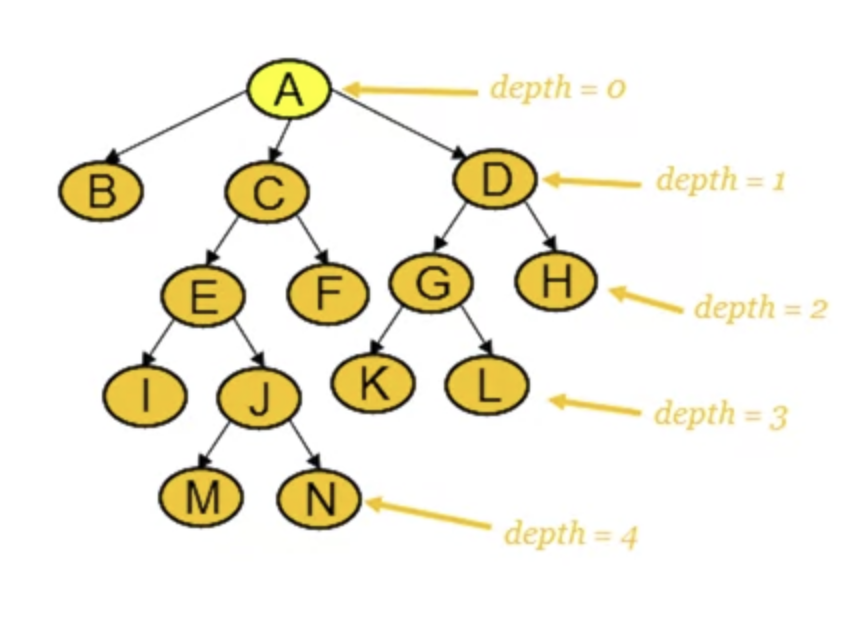
- Height of a node in a tree is the longest path from that node to the leaf.
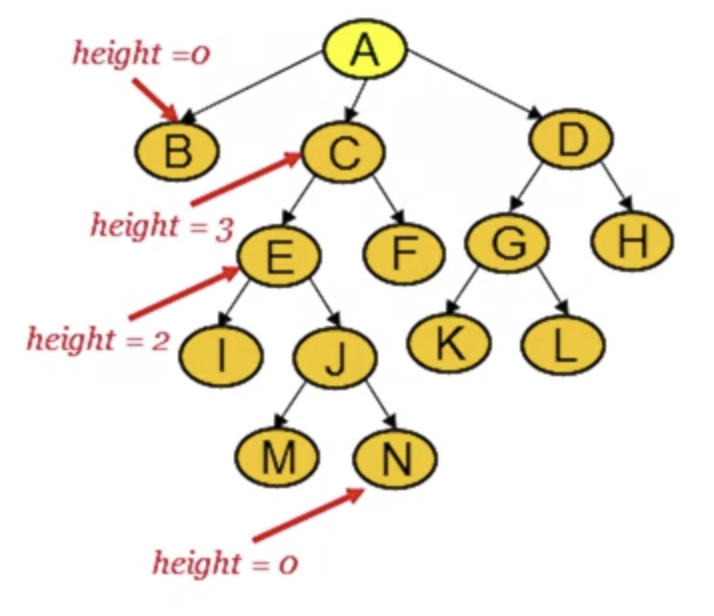
- The depth or the height of a tree is the maximum path length across all nodes.
- The depth (height) of this tree is 4.
- Special trees
-
Binary Tree is a rooted tree in which every vertex has 2 or fewer children.
-
Ternary tree is a rooted tree in which every vertex has 3 or fewer children.
- m-ary tree is a rooted tree in which every vertex has m or fewer children.
- Regular rooted trees
- A regular m-ary tree is regular if everyone of its node has exactly m children.
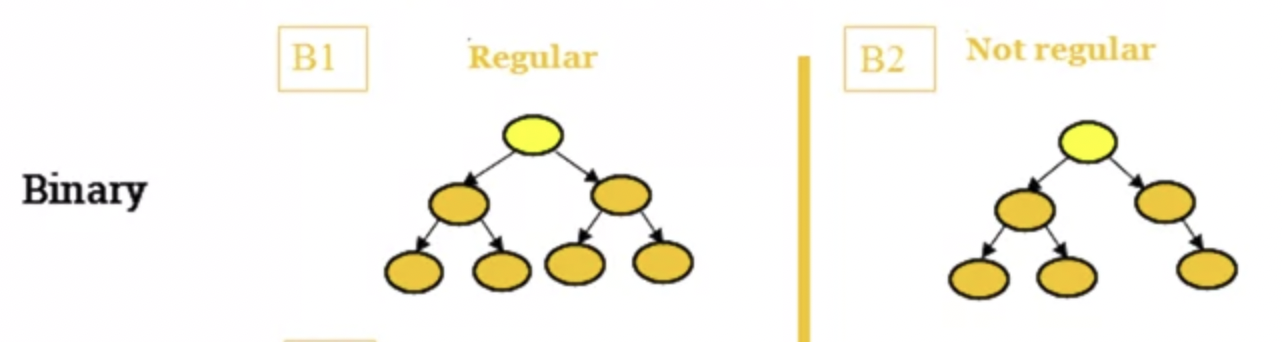
- Properties
-
m-ary tree has at most vertices as level h.
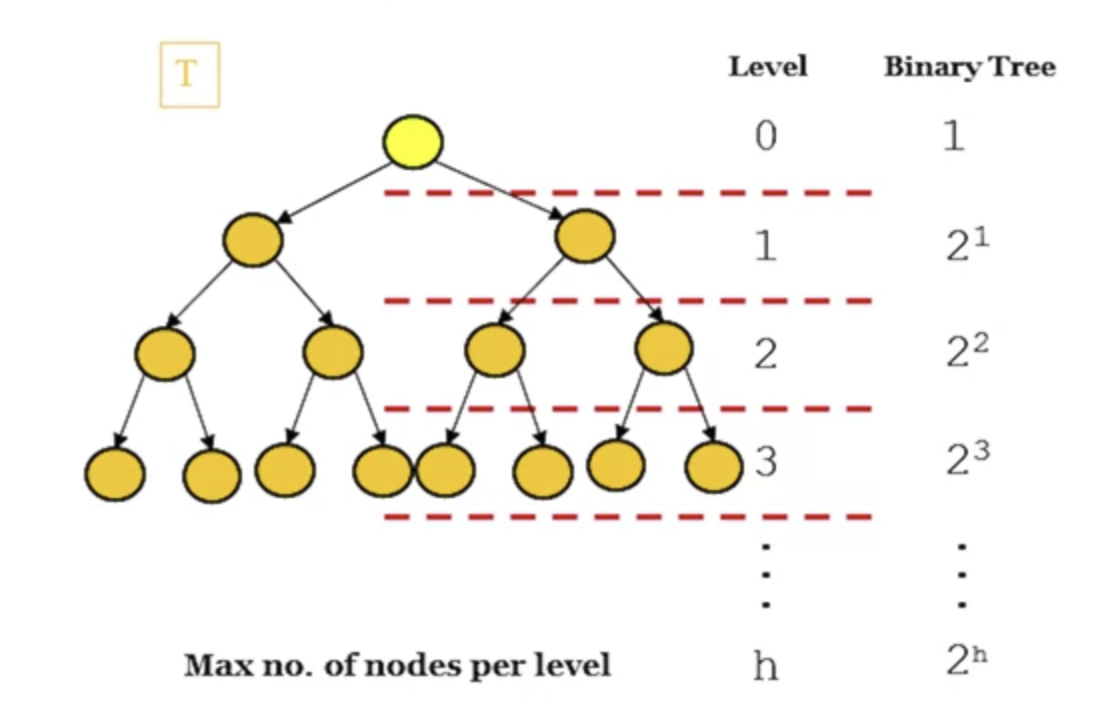
-
-
-
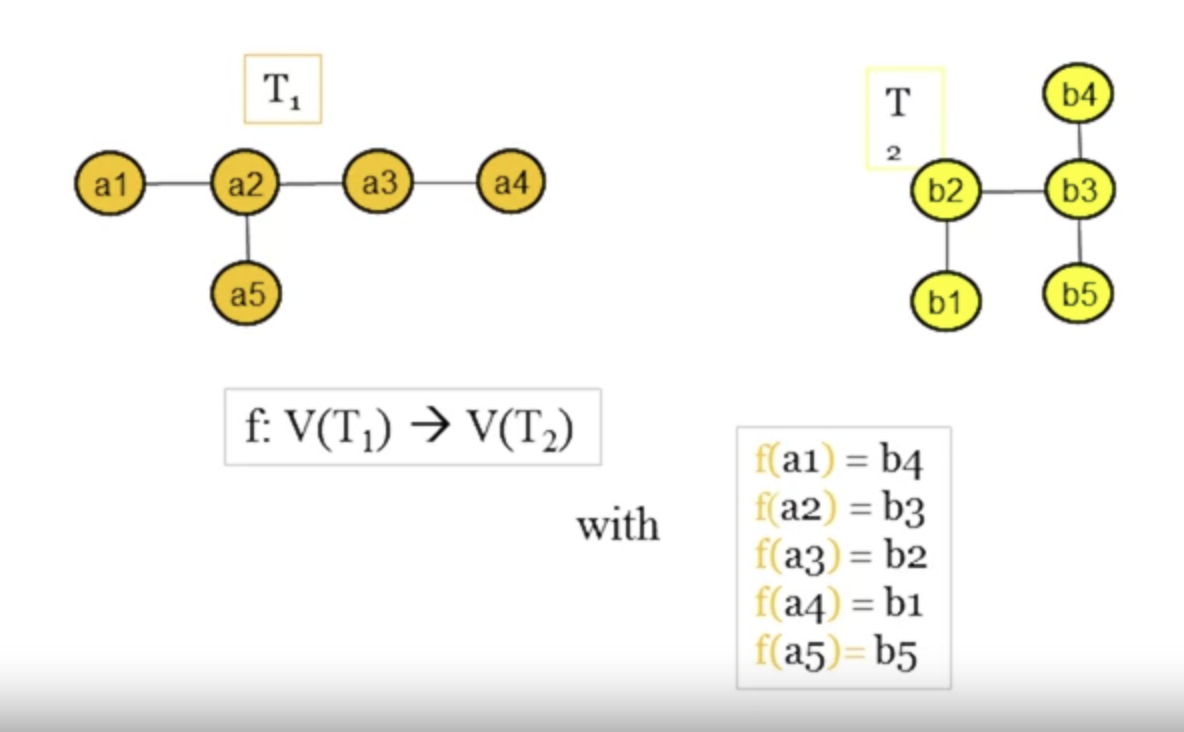
- 2 trees and are isomorphic if there is a bijection: which preserves adjacency and non-adjacency.
- That is, if uv is an edge in and is in
- Notation
- means that and are isomorphic.
- Example
-
Properties
- The properties of graphs also apply to trees.
- 2 trees with different degree sequences are not isomorphic.
- 2 trees with the same degree sequence are not necessarily isomorphic.
-
Isomorphic rooted trees
- Two isomorphic trees are isomorphic as rooted trees if and only if there is a bijection that maps the root of one tree to the root of the other.

8.203 Binary search trees
- A binary search tree with labels where they're larger on the right-hand side of the subtree and smaller on the left-hand side.
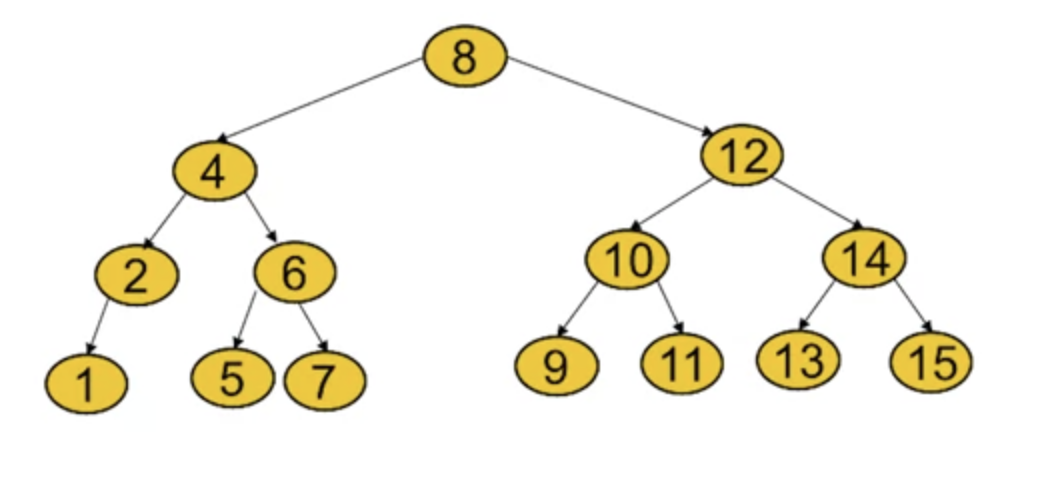
- Applications
- It's useful when we want to store a modifiable collection in a memory and be able to search, insert or remove elements from the collection efficiently.
- Binary search trees can be used to solve these kinds of problems.
-
Example
- Build a binary search tree to store 15 records
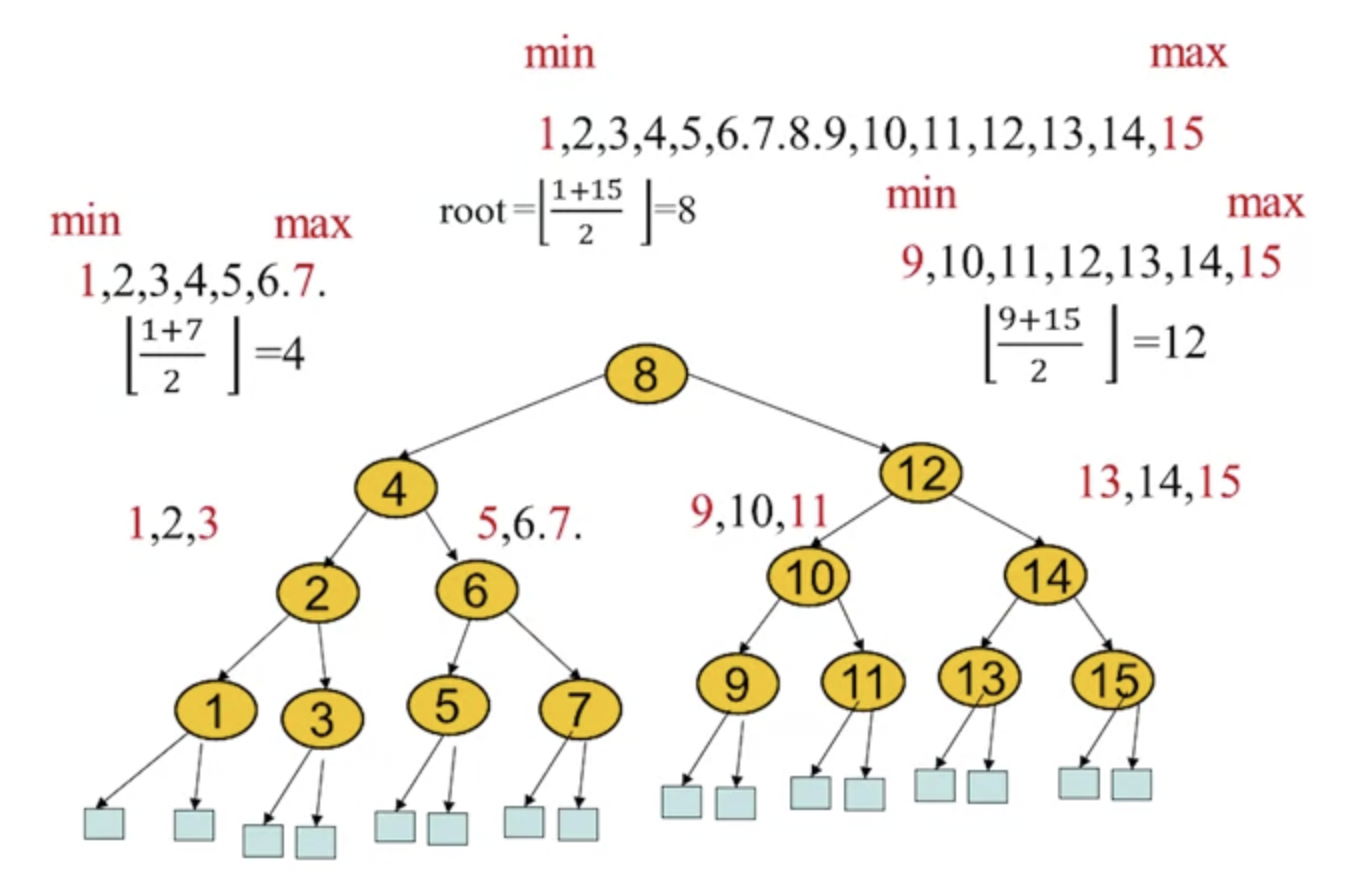
-
Height of a bst
- 2 methods for finding the height: * Method #1 * Method #2
- Binary search algorithm
- Starts by comparing the search element to the middle term in the list.
- The list is then split into 2 smaller sub-lists of the same size, or where one of these smaller lists has one fewer term than the other.
- Search continues by restricting the search to appropriate sub-list.
Peer Review
Question 1
Consider the following graph, G, with 4 vertices, , , and .
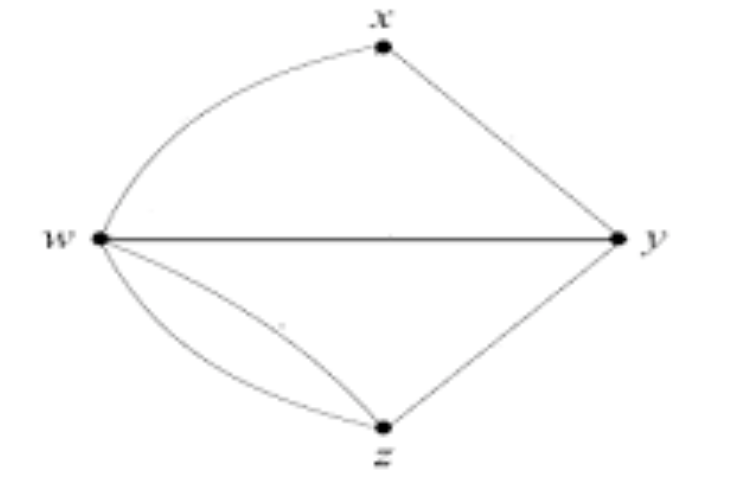
- Find the degree sequence of the graph .
4, 3, 3, 2
- Draw two non-isomorphic spanning trees of G.
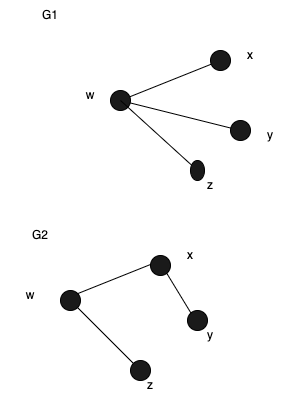
- Let be the adjacency matrix of . Write down .
$$ A = \begin{bmatrix} \ & w & x & y & z \
w & 0 & 1 & 1 & 2 \ x & 1 & 0 & 1 & 0 \ y & 1 & 1 & 0 & 1 \ z & 2 & 0 & 1 & 0 \end{bmatrix} $$
- What information does the sum of elements in A tell you about G?
The sum of elements is: From that information, we know that the numbers of edges is 12 / 2 = 6