Notes by Lex

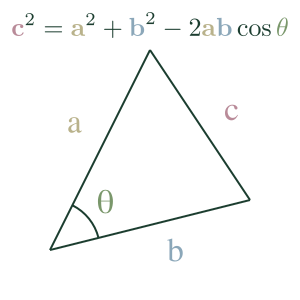
The Law of Cosines expresses the relationship between the length of a triangle's sides and one of its angles. For the cover triangle, the expression is:

$c^2 = a^2 + b^2 - 2ab \cos \theta$

We can use it to find the length of one side of a triangle if we know the opposite angle and length of the other sides.

$c = \sqrt{a^2 + b^2 - 2ab \cos \theta}$

We can also use it to find the angle, given the length of the triangle's sides.

$\cos \theta = \frac{a^2 + b^2 - c^2}{2ab}$

or

$\theta = \arccos(\frac{a^2 + b^2 - c^2}{2ab})$

An interesting note is that $\cos(90°) = 0$, so when you have a right triangle, we can simplify the expression to:

$c^2 = a^2 + b^2$

...which is the Pythogorean theorem.

KhanAcademyLabs (2013)