Week 13 - Graphs A
7.1 - Introduction to graph theory: basic concepts
- Computer scientists create abstractions of real world problems for representing and manipulating with a computer.
- One example, is logic which is used to define a computer circuits.
-
Scheduling final exams is another example:
- Has to take into account associations between courses, students and rooms.
- These associations (connections) between items are modelled by graphs.
-
- Discrete structures consisting of vertices (nodes) and edges connecting them.
- Graph theory is an area in discrete math which studies these type of discrete structure.
- What is a graph?
- Graphs are discrete structures consisting of vertices (nodes) and edges connecting them.
- Graph theory is an area that studies these structures.
- Origins of graph theory:
- First problem in graph theory is Seven Bridges of Konigsbert problem solved by Loenhard Euler in 1735.
- 2 islands are connected by 7 bridges.
- Can you walk across all 7 bridges only once.
- In a paper published in 1726, he showed that it is impossible.
- First problem in graph theory is Seven Bridges of Konigsbert problem solved by Loenhard Euler in 1735.
- Applications of graphs
- Used in a variety of disciplines.
- Examples:
- Networks.
- Road maps.
- Solving shortest path problems between cities.
- Assigning jobs to employees in an organisation.
- Distinguishing chemical compound structures.
Lesson 7.103 - Definition of a graph
- [Graph Theory.png](../../../../_media/week-13-complete-graphs](../../../../permanent/graph.md)
- Discrete structures consisting of vertices and edges connecting them.
- Formal definition:
- is an ordered pair .
- is a set of nodes, or vertices.
- is a set of edges, lines or connections.
-
- Basic element of a graph.
- Drawn as a node or a dot.
-
Set of vertices of G is usually denoted by V(G) or V.
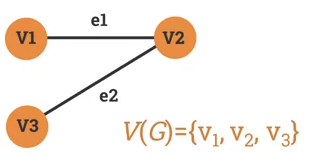
-
- A is a link between 2 vertices.
- Drawn as a line connecting two vertices.
-
A set of edges in a graph is usually denoted by or .
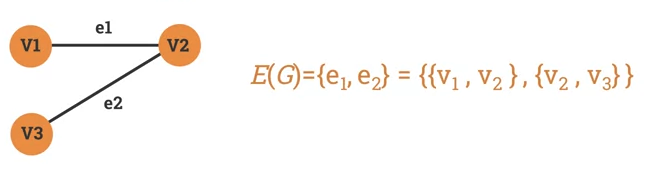
-
- Two vertices are said to be adjacent if they are endpoints of the same edge.
- Two edges are said adjacent if they share the same vertex.
-
If a vertex v is an endpoint of an edge e, then we say that e and v are incident.
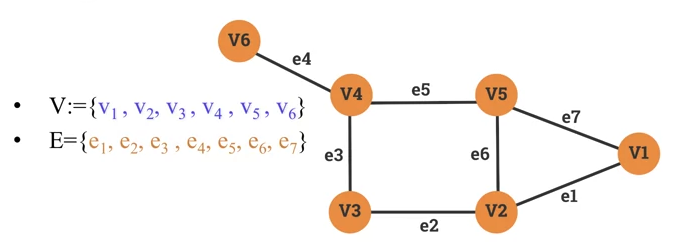
-
, are endpoints of the edge . We say that and are adjacent.
- The edges and share the same vertex . We say that and are adjacent.
- The vertex is an endpoint of the edge . We say that and are incident.
-
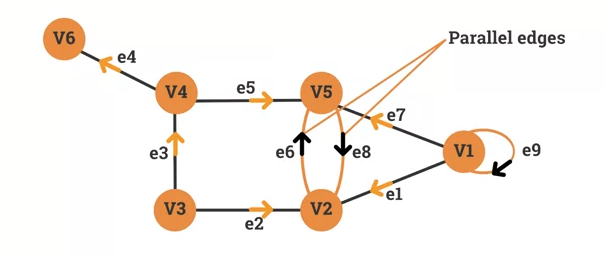
Loops and parallel edges
-
Consider this graph:
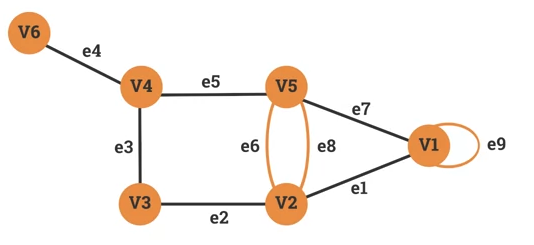
-
and are linked with 2 edged: (e_6 and e_8). e_6 and e_8 are considered Parallel Edges.
- is linked by . We call the edge a Loop.
- Directed Graphs
- Aka digraph.
- Graph where edges have a direction.
-
-
is a connection from to but not from to
- is a connection from to whereas is a connection from to .
Lesson 7.105 Walks and paths in a graph
-
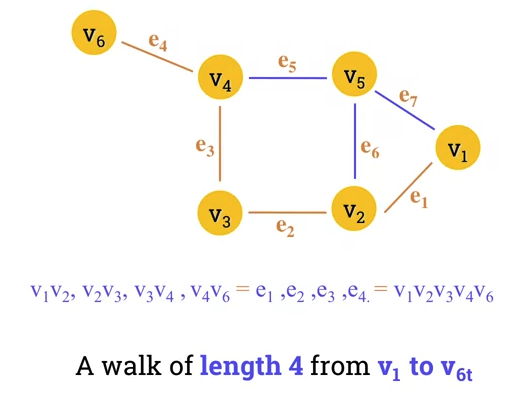
Definition of a Graph Walk
- Sequences of vertices and edges of a graph.
- Vertices and edges can be repeated.
- A walk of length k in a graph is a succession of (not necessarily different) edges of form:
- , , , ...,
- Example
-
Example 2
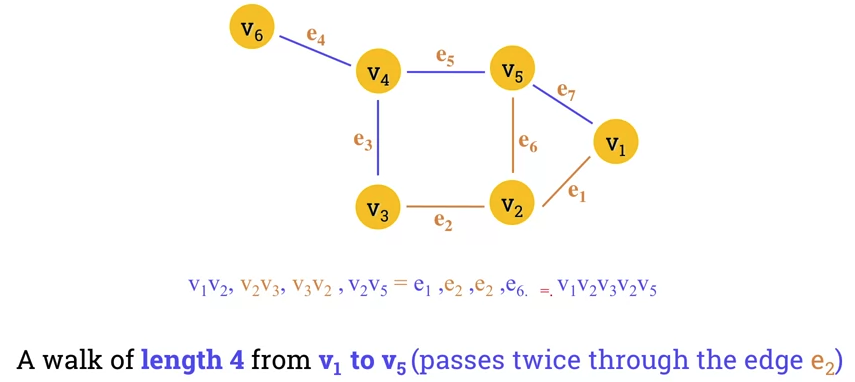
- Sequences of vertices and edges of a graph.
-
- A trail is a walk where no edge is repeated.
- In a trail, vertices can be repeated but no edge is repeated.
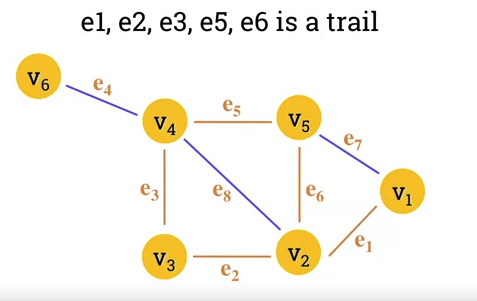
-
- A circuit is a closed trail.
- Circuits can have repeated vertices only.
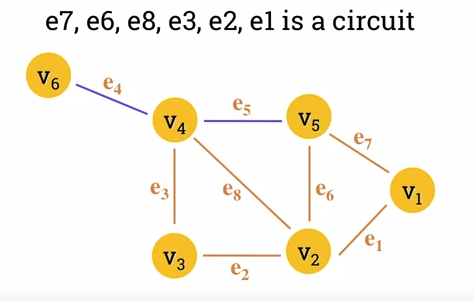
-
- A path is a trail in which neither vertices nor edges are repeated.
- Length of path is given in number of edges it contains.
-
- Closed path consisting of edges and vertices where a vertex is reachable from itself.
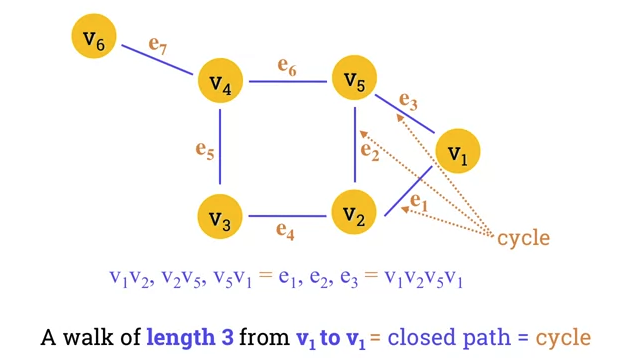
- Closed path consisting of edges and vertices where a vertex is reachable from itself.
-
Seven Bridges of Koenigsberg
- Is there a walk that passes each of the 7 bridges once.
- He made a network linked with lines that shows:
- No walk that uses each edge exactly once (even if we allow the walk to start and finish in diff places)
-
-
A Eulerian path in a graph is a path that uses each edge precisely once.
- If the path exists, the graph is called traversable.
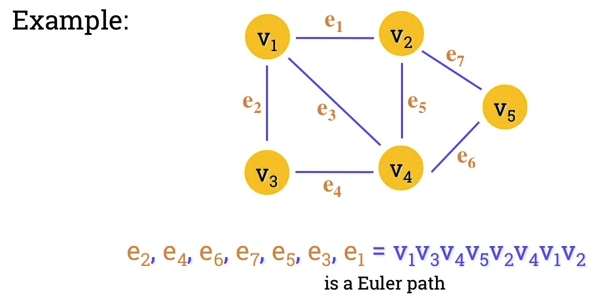
-
-
Hamiltonian path
- Hamiltonian path (aka traceable path) is a path that visits each vertex exactly once.
- A graph that contains a Hamiltonian path is called a traceable graph.
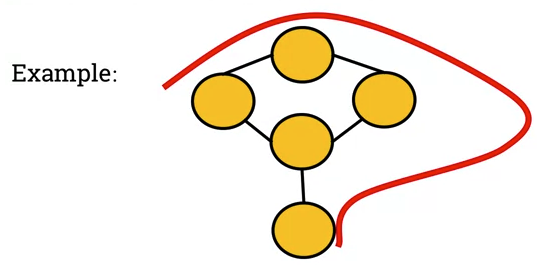
-
Hamiltonian cycle
- A Hamilton cycle is a cycle that visits each vertex exactly once (except for the starting vertex, which is visited once at the start and once again at end).
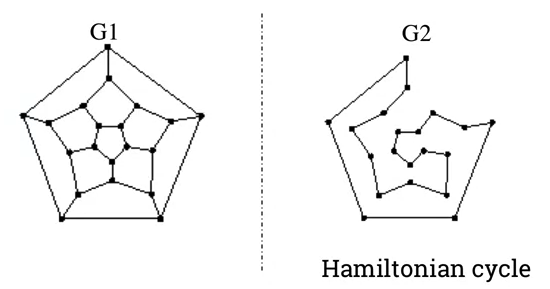
-
Connectivity
- An undirect graph is connected if
- You can get from any node to any other by following a sequence of edges OR
- any two nodes are connected by a path.
- Example of connected graph:
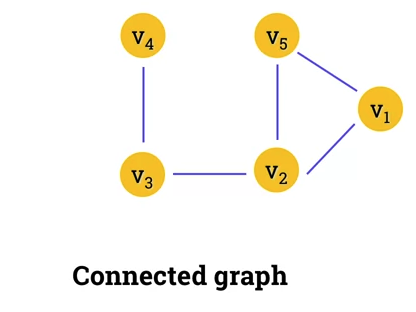
- An undirect graph is connected if
-
Unconnected graph
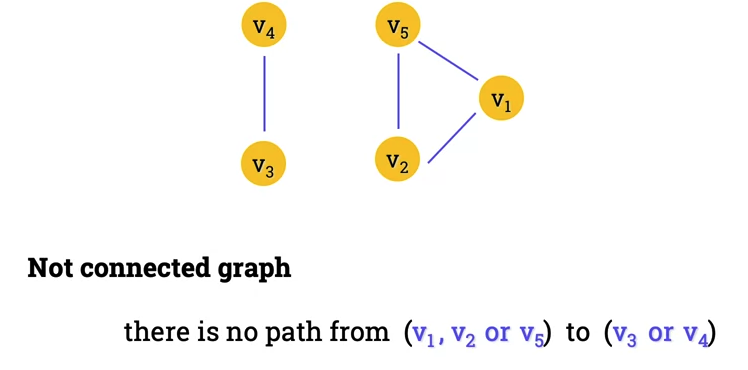
-
Strong connectivitiy
- A directed graph is strongly connected if there is a directed path from any node to any other node.
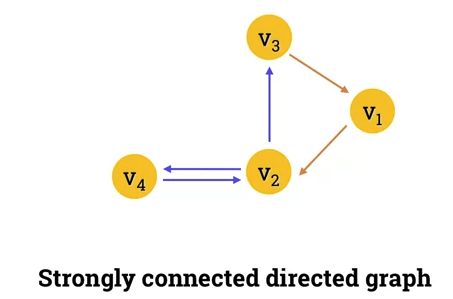
-
Example of a graph that's not strongly connected
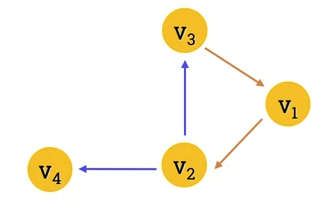
- No direct path from v_4 to any of the other 3 vertices.
- Transitive Closure
- Given a digraph G, the transitive closure of G is the digraph G such that: G has the same verticies as G
- If G has a directed path from to ($u \ge v$), G* has a directed edge from to .
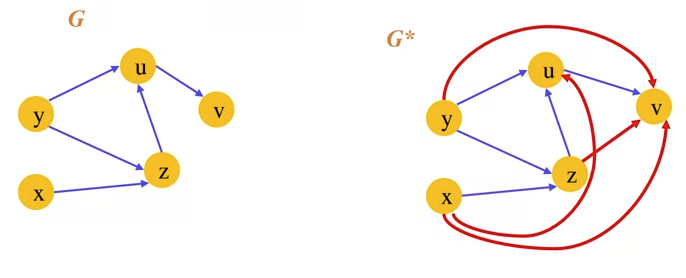
- Transitive closure provides reachability information about a digraph.
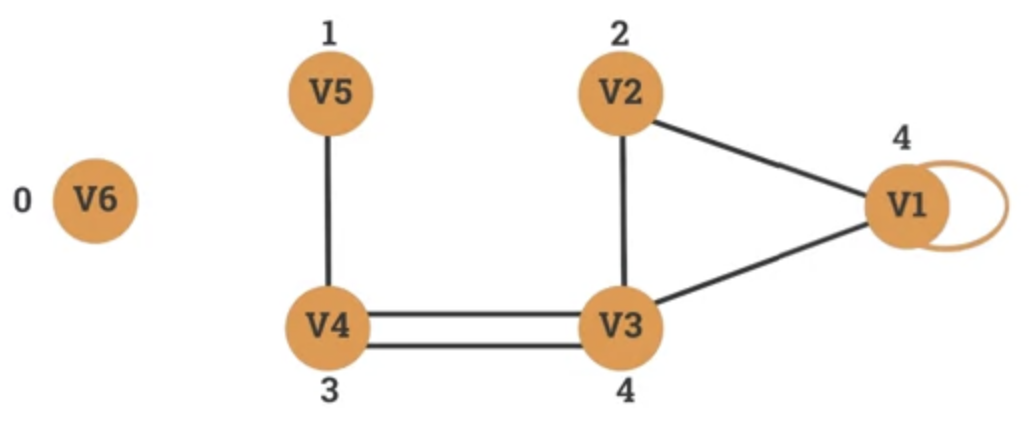
Lesson 7.107 - The degree sequence of a graph
-
- The number of edges incident on v.
- A loop contributes twice to the degree.
- An isolated vertex has a degree of 0.
-
For directed graphs:
- In-deg (v): number of edges for which v is the terminal vertex.
- Out-deg (v): number of edges for which v is the initial vertex.
- deg(v) = Out-deg(v) + In-deg(v)
- A loop contributes twice to the degree, as it contributes 1 to both in-degree and out-degree.
-
- Given an undirected graph G, a degree sequence is a monotonic nonincreasing sequence of the vertex degress of all the vertices G.
-
Properties of graph degree sequence:
- Degree sequence property 1
- The sum of degree sequence of a graph is always even.
- It is impossible to construct a graph where the sum of degree sequence is odd.
- The sum of degree sequence of a graph is always even.
-
Degree sequence property 2
- Given a graph G, the sum of the degree sequence of G is twice the number of edges in G.
- Number of edges(G) = (sum of degree sequences of G) / 2
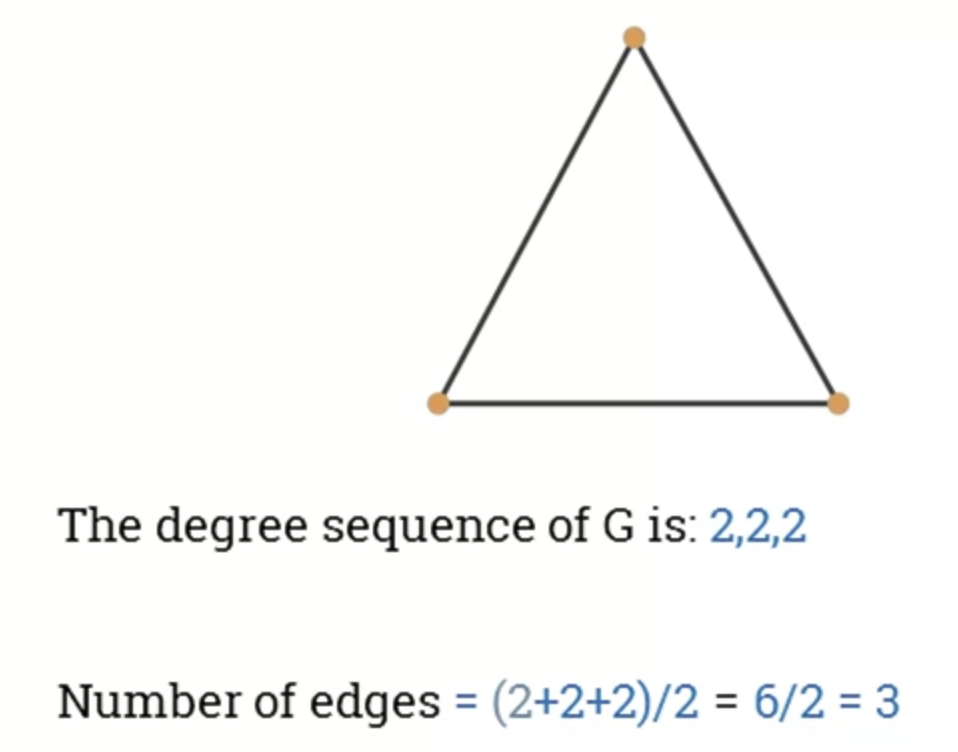
- Degree sequence property 1
-
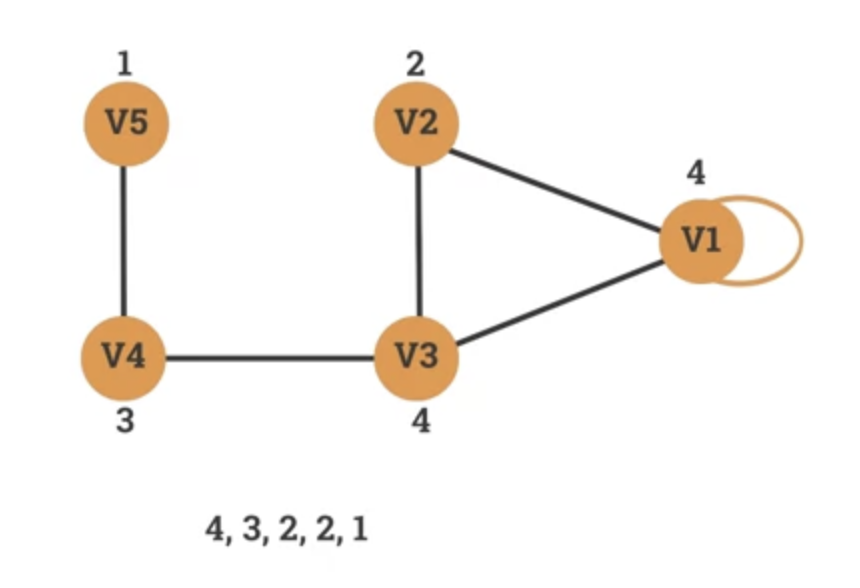
Exercise: which of the 2 degree sequences below is it possible to construct a graph with?
- 3, 2, 2, 1
- Sum of sequence = 3 + 2 + 2 =1 = 8
- Can build a graph with this.
- Number of edges = 8/2 = 4
- 3, 3, 2, 1
- Sum of sequence = 3 + 3 + 2 + 1 = 9
- Can't build a graph with this.
- 3, 2, 2, 1
7.109 - Special graphs: simple, r-regular and complete graphs
-
- A graph without loops and parallel edges.
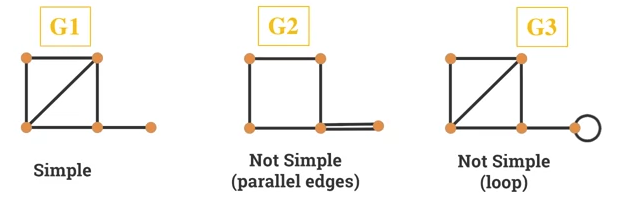
- Given a simple graph G with n vertices, then the degree of each vertex of G is at most equal to n-1.
- Proof
- Let be a vertex of G such that deg(v) > n-1
- However, we have only n-1 other vertices for v to be connected to.
- Hence, the other connections can only be a result of parallel edges or loops
- Exercise
- Can we draw a simple graph with the following degree sequences?
- 4, 2, 2, 2
- Sum(deg sequence) is even so we can construct a graph
- However, no other vertex has degree of 4. There are only 3 other vertices to be connected to, so it has to contain a loop or parallel edges.
- 4, 3, 3, 2, 2
- Yes, it can be done.
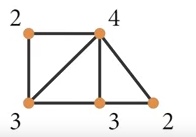
- Yes, it can be done.
- 4, 2, 2, 2
-
Regular Graph and R-Regular Graph
- A graph is regular if all local degrees are the same number.
- A graph G where all vertices the same degree, , is called a r-regular graph.
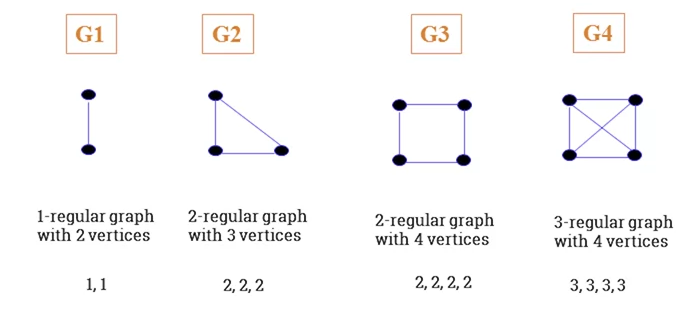
-
Given a r-regular G with n vertices, then the following is true:
- Degree sequence of
- Sum of degree sequence of
- Number of edges in
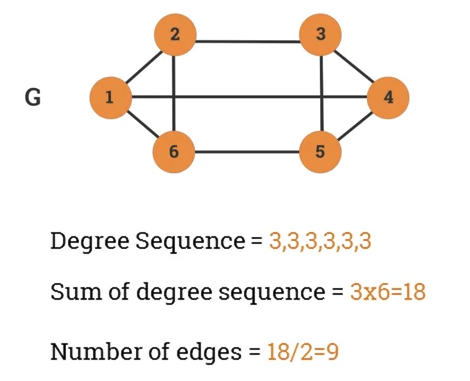
-
Special regular graphs: cycles

- Exercise
- Can we construct a 3-regular graph with 4 vertices?
- Can we construct a 4-regular graph with 5 vertices?
- 3x5 = 15
- Sum is odd, so cannot great a regular graph.
-
- A Simple Graph where every pair of vertices are adjacent (linked with an edge).
- A vertex on its own is a complete graph.
![week-13-complete-graph.png.png)
- A complete graph with n vertices, k_n, has these properties:
- Every vertex has a degree
- Sum of degree sequence
- Number of edges