Week 3 - Functions A
2.101 Introduction
- Variable
- In everyday life, many quantities depend on change in variables:
- Plant's growth depends on sunlight and rainfall.
- A runner's speed == how long it takes to run a distance.
- In everyday life, many quantities depend on change in variables:
2.102 The definition of a function
- Function
- A function is a rule that relates how one quantity depends on another.
- It's central to programming and Computer Science.
- It's a relationship between a set of inputs and a set of outputs, where inputs map to exactly one output.
- Function is a "well-behaved relation"
- Given a starting point, we have just one ending point.
- A function from a set of to a set of is an assignment of exactly one element of to each element of .
- If is the function from A to B, we write:
- We can read this as f maps A to B:
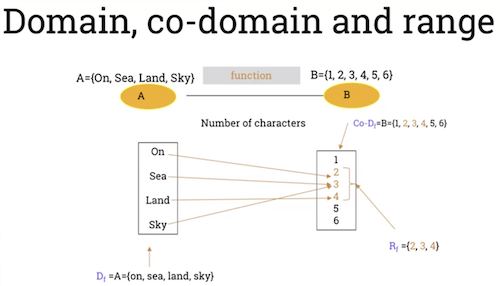
- Domain of a Function
- Given the function above, is the set of all inputs and called the "domain" of .
- Written as
- Given the function above, is the set of all inputs and called the "domain" of .
-
Co-Domain of Function
- is the set containing the outputs and called the co-domain of .
- Written as
- The set of all outputs is called the range of f and is written as .
- is called the image of .
-
is called the pre-image of .
-
Example: a set mapping characters to a length.
- (contains 3 characters)
- (contains 4 characters)
- 2 is the image of "on"
- "on" is the pre-image of 2.
- Conditions under which a relation is not a function:
- Some inputs do not have an image.
- Some inputs have more than one image.
- Exercise 1
- Given the following function: with , what is domain, co-domain and range for function ?
- Domain:
- Co-domain:
- Range:
- Exercise 2
- Given the following function: with
- Domain: R
- Co-domain: R
- Range:
- Pre-images(5) = {-2, 2}
- is the set containing the outputs and called the co-domain of .
2.104 Plotting functions
-
-
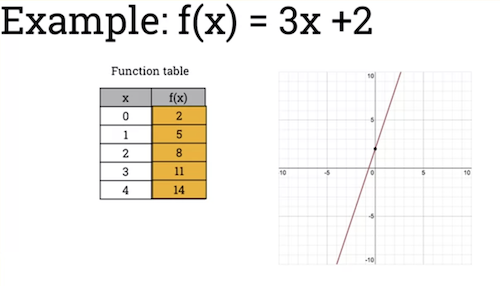
Linear function is of form:
- Where and are real numbers.
- Straight-line function that passes through point (0, b).
- is the gradient of the function. Where the function is increasing.
- That is: then .
- Example of increasing linear function:
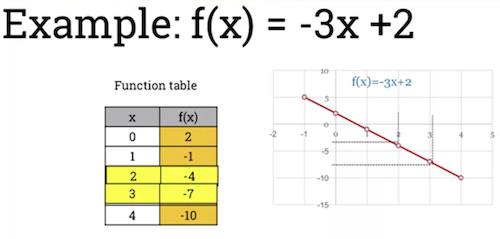
- When the gradient is < 0, the function is decreasing.
- If then function is increasing.
-
If then
-
-
-
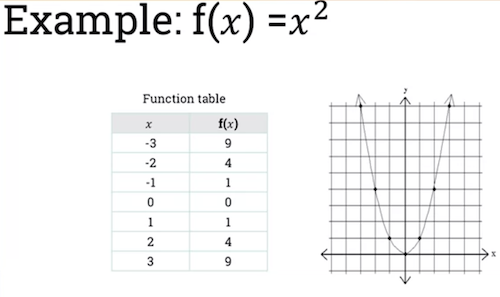
Quadratic functions:
-
Where , and are real numbers and .
-
Domain of function f(x) is set of real numbers.
- Range of function is set of positive numbers.
- Exponential Functions
- If base in , then function is increasing and represents growth shown in this graph:
-
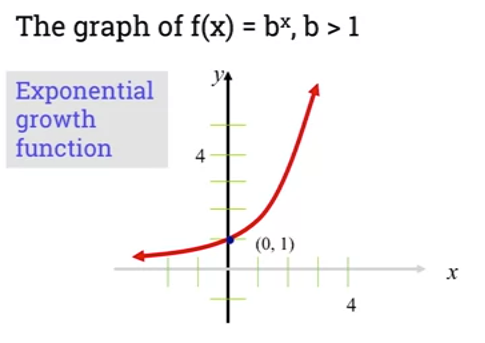
* Graph also shows that the point $(0,1)$ is a "common point". * Domain is equal to set of all real numbers. * Range is equal to set of all real positive numbers. * X-axis is horizontal asymtot to curve of function.-
If base 0 < b < 1, then function is decreasing:
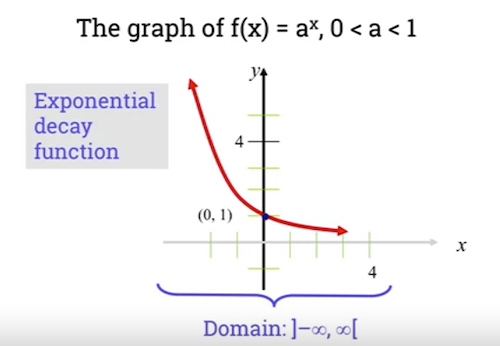
- Domain and range are the same as previous function.
- Laws Of Exponential Functions
-
2.106 Injective and surjective functions
-
-
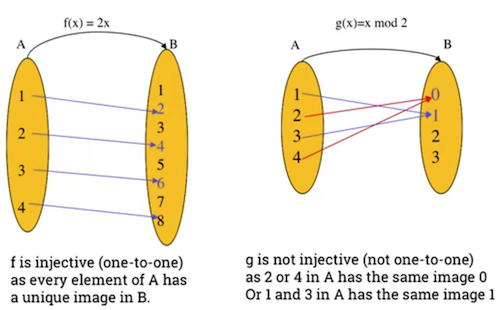
A function is considered injective or one-to-one if and only if:
- any 2 distinct inputs will lead to 2 distinct outputs.
- In other words:
- for all
- same as saying:
- Example on the left is an injective function, as every element of has a unique image in B.
- Example on the right is not injective. 2 or 4 in A have the same image 0. 1 and 3 have the same image 1.
-
You can show a function is not injective by finding two different inputs and with the same Function Image.
- An example with a linear function:
- To show function with is an injective function, we must show that
- => => => => f is injective.
- Proof 2:
- Let , show that
- => => => => f is injective
- Let , show that
- To show function with is an injective function, we must show that
- An example quadratic function that is not injection.
- Show function with is not an injective function
- Example with 2 counter examples that have the same image.
- One example is 5 and -5 have the same image.
- Since: it's not injective.
- If we change domain to , the function becomes injective.
- Proof 1:
- Let show that if then .
- Let show that if then
- Let show that if then .
- Proof 2:
- Let show that if then
- as is injective.
- One example is 5 and -5 have the same image.
- Surjective Function
- A function is said to be a surjective (onto) function if and only if every element of the co-domain of , , has at least one pre-image in the domain of .
- In other words, every element in the output domain has some input that will return it.
-
for all there exists such that
- Equivalent to saying range and co-domain of surjective function are the same.
-
Examples:
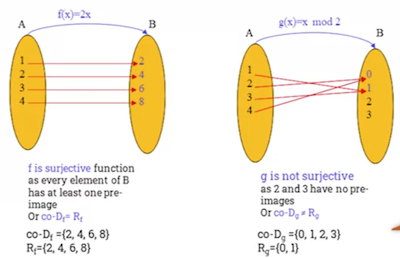
- Equivalent to saying range and co-domain of surjective function are the same.
-
An example Linear Function
- Show that the function with is a surjective (onto) function.
- Need to show that for any element , there exists such that
- Proof:
- => => =>
- Hence, for all , there exists such that
- An example quadratic function that is not surjective
- Show that function with not a surjective (onto) functions
- Proof: * Let , show that there exists such that * * We know the range of is positive integers only: all negative images have no pre-images.
- Examples:
- Injective, not surjective
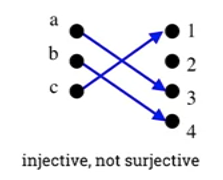
- Injective because each element in the domain has a unique image.
- Not surjective because the element 2 in the co-domain has no pre-image.
- Surjective but not injective
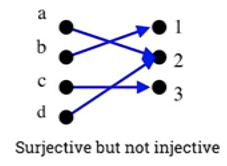
- Not injective because a and d are different but have the same image.
- Injective and surjective
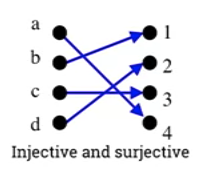
- Each element has a unique image.
- Each element in co-domain has at least one pre-image.
- Neither injective nor surjective
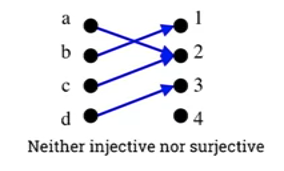
- Not injective because a and c have the same image.
- Not surjective because the 4 element of co-domain has no pre-image.
- Not a valid function
- Input a has 2 outputs. In a function, an input can only have a single output.
-
2.109 Functions (Peer-graded Assignment)
Part 1
- *$f_1 : \mathbb{R} \rightarrow \mathbb{R}$ where
- Claim: This function is not injective.
- Proof:
- Let ,
- therefore the function is not injective.
- Claim: This function is not surjective.
- Proof:
- therefore, this function is not surjective.
- *$f_2 : \mathbb{R} \rightarrow [1, + \infty [ \text{ where } f(x) = x^{2} + 1$
- Claim: This function is not injective.
- Proof:
- Let ,
- therefore the function is not injective.
- Claim: This function is surjective.
- Proof:
- therefore, this function is surjective.
- Claim: This function is injective.
- Proof:
- for all there the function is injective.
- Claim: This function is surjective
- Proof:
- therefore, the function is surjective.
- Claim: This function is injective.
- Proof:
- therefore f is injective.
- Claim: This function is surjective.
- Proof:
- therefore the function is surjective.
- Claim: This function is injective.
- Proof:
- therefore is injective.
- Claim: This function is not surjective
- Proof:
- for all therefore this function is not surjective.
Part 2
Let with
-
Show that is bijection.
- Claim: is a bijective as it is both injective and surjective.
- Proof of injective:
- therefore the function is injective.
- Proof of surjective:
- therefore the function is surjective.
-
Find the inverse function .
-
Plot the curve of and in the same graph.
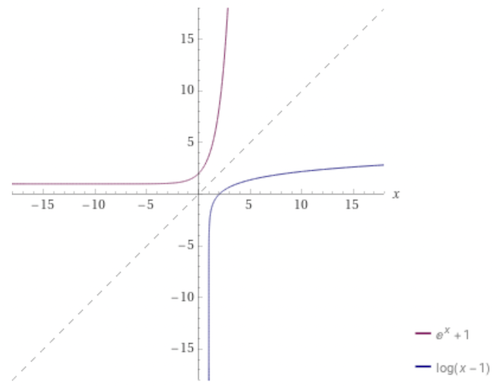
-
What can you say about these two curves?
The curves are symmetric with respect to the line .