Notes by Lex Toumbourou

2.202 Logical implication

• Logical Implication

  • Let $p$ and $q$ be propositions.
  • The conditional statement, or "implication $p \rightarrow q$" is the Proposition "if $p$ then $q$".
    • We call $p$ the hypothesis (or antecedent or premise)
    • We call $q$ the conclusion (or consequence)

  • Example:

    • Let $p$ and $q$ be the following statements:
      • $p$: "John did well in Discrete Mathematics."
      • $q$: "John will do well in the programming course."
    • The conditional statement $p \rightarrow q$ can be written as:
      • "If John did well in Discrete Maths then John will do well in programming."

    • Truth table for condition statement

      • If reasoning is correct (implication is true):
        • If the hypothesis is true then the conclusion is true
      • If reasoning is incorrect (implication is false):
        • if the hypothesis is true, the conclusion is false
      • it's always true that:
        • from a false hypothesis any conclusion can be implied (true or false)

      p	q	p -> q
      F	F	T
      F	T	T
      T	F	F
      T	T	T

  • Different expressions for $p$

    • Let $p$ and $q$ be the following statements:
      • $p$: it's sunny
      • $q$: John goes to the park
    • $p \rightarrow q$
      • if $p$ then $q$
      • if $p$, $q$
      • $p$ implies $q$
      • $p$ only if $q$
      • $p$ follows from $q$
      • $p$ is sufficient for $q$
      • $q$ unless $\neg p$
      • $q$ is necessary for $p$
  • Converse, contrapositive and inverse
  • Let $p$ and $q$ be propositions and $A$ the conditional statement $p \rightarrow q$
  • The proposition $q \rightarrow p$ is the converse of $A$.
  • The proposition $\neg p \rightarrow \neg q$ is the contrapositive of $A$
  • Example 1
    • Let $p$ and $q$ be the following statements:
      • $p$: It's sunny.
      • $q$: John goes to the park.
      • And $A$ the statement $p \rightarrow q$: "If it's sunny then John goes to the park"
    • The converse of A is: If John goes to the park then it's sunny.
    • The contrapositive of A is: If John doesn't go to the park, then it's not sunny.
  • Example 2
    • Let p and q be two propositions concerning an integer n
      • $p$: n has one digit
      • $q$: n is less than 10
    • Writing the statement using symbolic logic expression:
      • If the integer n has one digit then it is less than 10.
        • $p \rightarrow q$
    • Now write its contrapositive using both symbolic logic expression and English:
      • $\neg q \rightarrow \neg p$
      • If n is greater than or equal to 10, then n has more than one digit.

3.204 Logical equivalence

• Logical Equivalence
  • The biconditional or equivalence statement $p \leftrightarrow q$ is the proposition: $p \rightarrow q$ and $q \rightarrow p$
• Equivalence properties ($\leftrightarrow$)
  • Biconditional statements are also called bi-implications.
  • $p \leftrightarrow q$ can be read as "p if and only if q"
  • The biconditional statements is true when p and q have the same truth values, and is false otherwise.

$p$	$q$	$p \rightarrow q$	$q \rightarrow p$	$(p \rightarrow q \land q \rightarrow p)$ equivalent
F	F	T	T	T
F	T	T	F	F
T	F	F	T	F
T	T	T	T	T

• Equivalent propositions
  • Let $p$ and $q$ be propositions
  • $p$ and $q$ are logically equivalent if they always have the same truth value.
  • We write $p \equiv q$
  • The symbol $\equiv$ is not a logical operator, and $p \equiv q$ is not a compound proposition, but rather saying the statemnet that $p \leftrightarrow q$ is always true.
• Proving equivalence
  • To determine equivalence, we can use truth tables
  • Examples
    • Compare two propositions $p \rightarrow q$ and $\neg p \lor q$
    • The truth tables shows that $\neg p \lor q$ is equivalent to $p \rightarrow q$ as they have the same truth values.

$p$	$q$	$p \rightarrow q$	$\neg p$	$\neg p \lor q$
F	F	T	T	T
F	T	T	T	T
T	F	F	F	F
T	T	T	F	T

• Proving non-equivalence
  • To determine equivalence, we can use truth tables and find at least one row where values differ.
  • Example
    • Let's examine whether the converse or the inverse of an implication is equivalent to the original implication.

$p$	$q$	$\neg p$	$\neg q$	$p \rightarrow q$	$\neg p \rightarrow \neg q$	$q \rightarrow p$
F	F	T	T	T	T	T
F	T	T	F	T	F	F
T	F	F	T	F	T	T
T	T	F	F	T	T	T

• Example
  • Let $p$, $q$ and $r$ be the following propositions concerning an integer n:
    • $p$: n = 20
    • $q$: n is even
    • $r$: n is positive
  • Let's express each of the following conditional statements symbolically:
    • if $n = 20$ then $n$ is positive: $p \rightarrow r$
    • $n = 20$ if n is even: $q \rightarrow p$
    • $n = 20$ only if n is even: $p \rightarrow q$
• Precedence of logical operations
  • $\neg$ - 1
  • $\land$ - 2
  • $\lor$ - 3
  • $\rightarrow$ - 4
  • $\leftrightarrow$ - 5
• Summary
  • definition of equivalence
  • equivalence properties
  • equivalent propositions
  • proving equivalence
  • proving non-equivalence
  • precedence of logical operations

3.206 Laws of prospositional logic

• Laws of Propositional Logic

  • Propositional logic is an algebra involving multiple laws. These are some of the laws:

  	Disjunction	Conjunction
  idempotent laws	$p \lor p \equiv p$	$p \land p \equiv p$
  commutative laws	$p \lor q \equiv q \lor p$	$p \land q \equiv q \land p$
  associative laws	$(p \lor q) \land r \equiv p \lor (q \lor r)$	$(p \land q) \land r \equiv p \land ( q \land r)$
  distributive laws	$p \lor (q \land r) \equiv (p \lor q) \land (p \lor r)$	$p \lor (q \lor r) \equiv (p \land q) \lor (p \land r)$
  identity laws	$p \lor \mathbf{F} \equiv p$	$p \land \mathbf{T} \equiv p$
  domination laws	$p \lor \mathbf{T} \equiv \mathbf{T}$	$p \land \mathbf{F} \equiv \mathbf{F}$

  • Example

    

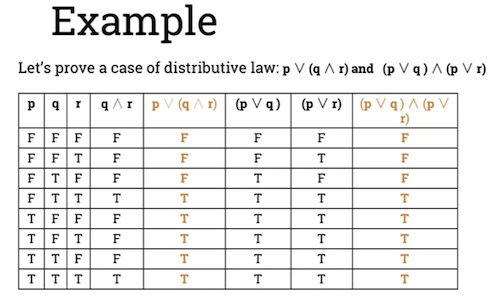
  • Laws of propositional logic 2

    

• Equivalence Proof

  • Example the equivalence between $\neg (p \land (\neg p \lor q))$ and $(\neg p \lor \neg q)$
  • $\neg (p \land (\neg p \lor q))$ - given proposition
  • $\neg p \lor \neg (\neg p \lor q)$ - De Morgan's law
  • $\neg p \lor ((\neg \neg p) \land \neg q)$ - De Morgan's law
  • $\neg p \lor (p \land \neg q)$ - double negation law
  • $(\neg p \lor p) \land (\neg p \lor \neg q)$ - distributive laws
  • $T \land (\neg p \lor \neg q)$ - complement laws

Problem Sheet

Question 1

Which of the following statements are propositions?

• *$2 + 2 = 4$ - is proposition
• 2 + 2 = 5 is proposition
• $w^2 + 2 = 11$ - is not a proposition,as value depends on the value of x
• $x + y > 0$ - is not a proposition, as value depends on x and y.
• "This coffee is strong" - is not a proposition. It is subjective, not true or false.

Question 2. Let $s$ and $i$ be the following propositions:

• $s$ - "stocks are increasing"
• $i$ - "interest rates are steady"
• Write each of the following sentences symbolically:
• Stocks are increasing but interest rates are steady. $s \land i$
• Neither are stocks increasing nor are interest rates steady.

$\neg s \land \neg i = \neg (s \land i)$

Question 3.

Let $h$, $s$ and $r$ be the following 3 propositions:

h: it is hot. s: it is sunny. r: it is raining.

1. It is not hot but it is sunny.

$\neg h \land s$

1. It is neither hot nor sunny

$\neg (h \lor s)$

1. It is either hot and sunny or it is raining

$(h \land s) \lor r$

1. It is sunny or it is raining but not both

$s \oplus r$

Question 4.

Let l denote one of the letters in the word "software". The following propositions relate to $l$

p: "l is a vowel". q: "l comes after the letter k in the alphabet".

Use the listing method to specify the truth sets corresponding to each of the following statements:

$p$: $\{o, a, e\}$ $q$: $\{s, o, t, w, r\}$ $\neg p$: $\{s, f, t, w, r, o\}$

• $\neg q$ = {f, a, e}
• $p \land \neg q$ = {a, e}
• $\neg p \lor q$ = {s, o, f, t, w, r}

Question 5.

Let $p$ and $q$ be 2 propositions. Construct a truth table to show the truth value of each of the following logical statements:

p	q	$p \lor q$	$\neg p$	$\neg q$	$\neg p \lor \neg q$	$p \land q$	$\neg (p \land q)$
T	F	T	F	T	T	F	T
T	T	T	F	F	F	T	F
F	T	T	T	F	T	F	T
F	F	F	T	T	T	F	T

We can see that $\neg p \lor \neg q$ and $\neg (p \land q)$ are equivalent statements (using De Morgan's Law).

Question 6.

Let $h$, $s$, and $p$ be the following 3 propositions:

$h$: it is hot $s$: it is sunny $r$: it is raining

1. It is sunny or it is raining but not both.

   $h \oplus r$

2. It is hot only if it is sunny.

   $h \rightarrow s$

3. It is hot only if it is sunny and not raining.

   $h \rightarrow (s \land \neg r)$

Question 7.

Let $p$, $q$ be propositions. Construct a truth table to show the truth value of each of the statements:

• *$p \rightarrow q$
• $\neg p \land q$
• $\neg q \rightarrow \neg p$

p	q	not p	not q	if p then q	not p or q	if not q then not p
T	F	F	T	F	F	F
T	T	F	F	T	T	T
F	T	T	F	T	T	T
F	F	T	T	T	T	T

$p \rightarrow q = \neg p \lor q = \neg q \rightarrow \neg p$

$\neg q \rightarrow \neg p$ is the contrapositive of $p \rightarrow q$

Question 8.

Let p and q be the following propositions concerning a positive integer $n$

p: n is divisible by 5. q: n is even.

1. Express in words the following statements:

$p \lor \neg q$

n is divisble by 5 or n is odd.

$p \land q$

n is divisible by 5 and n is even.

1. List the elemenst of the truth sets corresponding to each of the statements in (1).

$\{1, 3, 5, 7, 9, 10, 11, 13 ...\}$ $\{10, 20, 30, ...\}$

1. Express each of the following conditional statements symbolically.

if n is odd then n is divisible by 5.

$\neg q \rightarrow p$

n is even or n is divisible by 5 but not both.

$q \oplus p$

Question 9.

Let $p$ and $q$ be two propositions. Show that $p \lor \neg (p \land q)$ is a tautology.

• $p \lor \neg (p \land q)$ -- original expression
• $p \lor \neg p \lor \neg q$ -- De Morgan's law
• $p \lor \neg p = T$ = $T \land \neg q$ = T

Question 10.

Complete the following table by showing the truth value of each: $p$, $q$, $p \rightarrow q$, $q \rightarrow p$, $p \leftrightarrow q$

p	q	$p \rightarrow q$	$q \rightarrow p$	$p \leftrightarrow q$
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	1	1	1

Question 11.

What is the inverse, the converse and the contraposition of the following statement:

If it is November 5th then we have fireworks.

p: is it November 5th q: we have fireworks

Inverse

$\neg p \rightarrow \neg q$

If it's not November 5th then we don't have fireworks.

Converse

$q \rightarrow p$

If we have fireworks then it is November 5th

Contrapositive

$\neg q \rightarrow \neg p$

If we don't have fireworks then it's not November 5th.

Question 12.

Let p denote the following statement about integers n:

If n is divisible by 15, then it is divisible by 3 or divisible by 5.

Write the inverse, the converse and the contrapositive of p.

p: if n is divisible by 15, then it is divisble by 3 or divisible by 5.

s: divisible by 15 q: divisible by 3 r: divisble by 5

$s \rightarrow (q \lor r)$

Inverse:

$\neg s \rightarrow \neg (q \lor r)$

If n is not divisible by 15, then it is not divisible by either 3 or 5.

Converse:

$(q \lor r) \rightarrow s$

If n is divisble by either 3 or 5, then n is divisble by 15.

Contrapositive:

$\neg (q \lor r) \rightarrow \neg s$

If n is not divisble by either 3 or 5 then n is not divisible by 15.

Question 13.

Let p and q be two propositions. Show by constructing the truth table or otherwise that the following statements are equivalent:

$p \lor q$ and $\neg$