Week 9 - Boolean Algebra A
Lesson 5.1 The basics
Video: 5.101 Introduction to Boolean algebra
- Boolean Algebra
- History
- 384-322 BC: Aristotle develops the foundations of logic.
- 1854: George Boole published An investigation of the laws of thought
- 1904: H.E. Huntington wrote Sets of independent postulates for the algebra of logic.
- 1938: Claude Shannon wrote a thesis: A symbolic analysis of relay switching
- Boolean algebra is the foundation of computer circuit analysis.
- Basic building block for designing transistors, basic elements in processors.
- Consider IoT fire system: when high heat is detected, spray water.
- Two-valued Boolean Algebra
- Most well-known form of Boolean algebra is 2 valued system:
- variables take value in set
{0, 1} - operators
+and.correspond toORandAND.
- variables take value in set
- Used to describe and design digital circuits.
- Most well-known form of Boolean algebra is 2 valued system:
- History
- Operations of Boolean Algebra
- Based on 3 fundamental operations:
- AND
- logical product, intersection or conjunction
- represented as x . y, or .
- OR
- logical sum, union or disjunction
- represented as , ,
- NOT
- logical complement or negation
- represented as , or
- AND
- When parentheses are not used, orperators have order of prefs: NOT > AND > OR.
- Based on 3 fundamental operations:
- Operations of Boolean algebra
- The truth tables for the 3 operations can be represented as follows:
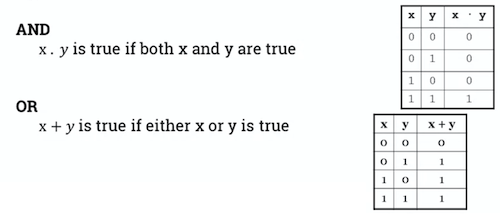
- The truth tables for the 3 operations can be represented as follows:
5.103 Postulates of Boolean algebra
- Huntington's Postulates
- Huntington's posulates define 6 axioms that must be satisfied by any Boolean algebra:
- closure with respect to the operators:
- any result of logical operation belongs to the set {0, 1}
- identity eleements with respect to the operators:
- commutativity with respect to the operators (dot and .):
- distributivity:
- commutativity
- distributivity
- complements exist for all elements
- distinct elements
- closure with respect to the operators:
- Huntington's posulates define 6 axioms that must be satisfied by any Boolean algebra:
-
Basic Theorems of Boolean Algebra
- Using the 6 axioms of Boolean algebra, we can find these useful theorems for analysing and designing circuits
- theorem 1: idempotent laws
- theorem 2: tautology and contradiction
- theorem 3: involution
- theorem 4: associative laws
- theorem 5: absorption laws
- theorem 6: uniqueness of complement
- if and then
- theorem 7: inversion law
- ,
- theorem 1: idempotent laws
-
De Morgan's Theorems
- Theorem 1
- The complement of a product of variables is equal to the sum of the complements of the variables:
-
Theorem 2
- The complement of a sum of variables is equal to the product of the complements of the variables:
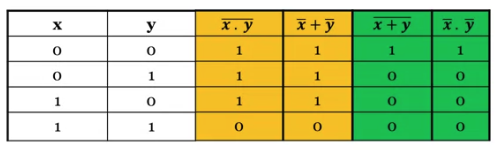
- Theorem 1
-
Proof of distributivity of + over .
- A truth table to prove the distributivity of + over . using truth tables.

- A truth table to prove the distributivity of + over . using truth tables.
- Principle of duality
- Starting with a Boolean relation, we can build another equivalent Boolean relation by:
- changing each OR (+) sign to an AND (.) sign
- changing each AND (.) sign to an OR (+) sign.
- changing each 0 to 1 and each 1 to 0.
- Example
- Since A + BC = (A + B)(A + C) (by distributive law), we can build another relation using the duality principle:
- Examples
- Consider the boolean equations:
- e2:
- Dual equations of e1 and e2:
- Dual of e1:
- Dual of e2:
- Consider the boolean equations:
- Starting with a Boolean relation, we can build another equivalent Boolean relation by:
- Ways of proving theorems
- 4 ways in general to prove equivalence of Boolean relations:
- perfect induction by showing 2 expressions have identical truth tables: tedious if more than 2 vars.
- axiomatic proof by applying Huntington's postulates or theorems to the expressions, until identical expressions are found.
- duality principle every theorem in Boolean algebra remains valid if we interchange all ANDs and ORs and interchange all 0s and 1s.
- contradiction by assuming the hypothesis is false then proviing that the conclusion is false.
- Examples
- Proving absorption theorem
- The absorption theorem can be proved using perfect induction, by writing a truth table.
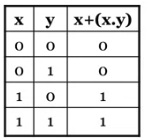
- It can also be proved directly:
- From , if we apply the duality principle, we can deduce:
- The absorption theorem can be proved using perfect induction, by writing a truth table.
- Proving absorption theorem
- Using the 6 axioms of Boolean algebra, we can find these useful theorems for analysing and designing circuits
\begin{align} x + (x . y) &= (x . 1) + (x . y) \text{ by } x .1 = x \\ &= x . (1 + y) \text{ by distributivity } \\ &= x . (y + 1) \text{ by commutativity } \\ &= x . 1 \text{ by } y + 1 = 1 \\ &= x \text{ by } x.1 = x \\ \end{align}
5.105 Boolean functions
- Boolean Function
- A boolean function defines a mapping from one or multiple Boolean input values to a Boolean output value.
- For Boolean input values, there are possible combinations.
- For example, a 3-input function can be completely defined with an 8-row truth table.
- Algebraic forms
- There is only one way to represent a Boolean function in a truth table.

- In algebraic form, a function can be expressed in a variety of ways:
- For example these are both algebraic representations of the same truth table:
- For example these are both algebraic representations of the same truth table:
- There is only one way to represent a Boolean function in a truth table.
- Standardised forms of a function
- The two most common standardised forms:
- sum-of-products form
- product-of-sums form
- Sum-of-Products Form:
- Variables built using the
ANDoperator, are summed together using theORoperator. - Example:
- Variables built using the
- Product-of-Sums Form
- Variables built using the
ORoperator, are multiplied together using theANDoperator. - Example:
- Variables built using the
- The sum-of-products form is easier to use so it's used by the course.
- The two most common standardised forms:
- Building a sum-of-products form
-
- Focus on the values of the variable that make the function equal to .
-
- If an input equals , it appear uncomplemented in the expression.
-
- If an input equals 0, it appears complemented in the expression (and its corresponding complete is used).
-
- the function f is then expressed as the sum of products of all the terms for which f = 1
- Example
- Let's consider the function f represented by the following truth trable.
- Can be expressed as:
- Can be expressed as:
- Let's consider the function f represented by the following truth trable.
-
- Useful functions
- The "exclusive-or" function: :
- defined as "true if either x or y is true, but not both"
- represented by this truth table:
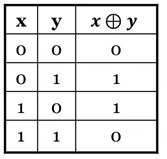
- can be expressed as:
- The "implies" function: :
- defined as "if x then y"
- represented by this truth table:
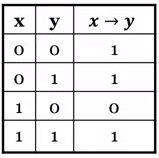
- can be expressed as:
- The "exclusive-or" function: :