Basic geometry: language and labels

Nov 04, 2020 reference/videos

Notes from Khan Academy video Basic geometry: language and labels | Introduction to Euclidean geometry | Geometry | Khan Academy

  • Word geometry is made up of 2 components: "geo" and "metry":
    • "Geo" - earth
    • "metry" - measurement
    • Therefore, geometery is about how shapes and space (things we see) related to each other.

Plane

  • A plane is a flat surface that has 2 dimensions: width and height and goes on infinity in either direction.

Point

  • A point refers to a dot on that plane and is the most basic geometric idea.

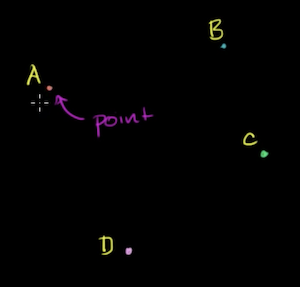
    points on a plane

    • points are commonly labelled using upper case letters: A, B, C, D etc

    • A point is said to be 0-dimension: it doesn't provide any direction information.

Line Segment

  • A line that connects 2 points, is refered to as a line segment

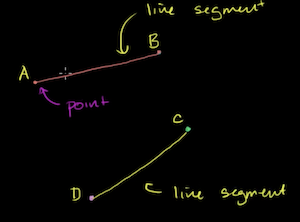
    line segment examples

    • A line segment is described using its endpoints: the points that it is connected by.

    • In math notation, a line is drawn over the endpoints to denote that it's a line segment.

      AB‾\overline{AB}

    • The endpoints of a line segment can be inversed:

      AB‾=BA‾\overline{AB} = \overline{BA}

    • A line segment is one-dimension - you can move back and forth along it.

Ray

  • A line that starts from one point that continues on infinitely in one direction is called a Ray

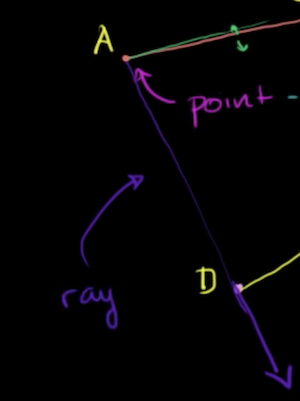
    ray example

    • The order of a ray is meaninful, unlike a line segment, as it describes the direction of the ray:

      AB→≠BA→\overrightarrow{AB} \neq \overrightarrow{BA}

    • The starting point is referred to the endpoint

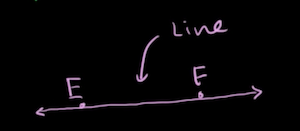
Line

  • A line that continues infinitely in either direction is formally called a line.

    line example

    • A line is described by the endpoints it intersects, typically in alphabetical order though the order does not matter.

      AB↔=BA↔\overleftrightarrow{AB} = \overleftrightarrow{BA}

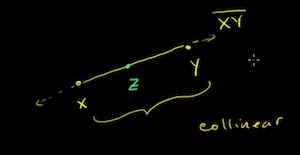
Collinear points

  • If you have a line segment and introduce a point in the middle, you could describe all 3 points as "collinear" - they sit on the same line.

    colinear points example

  • In the above picture, if the distance between XZXZ was the same as the distance between ZXZX, then you would refer to Z as the midpoint of the line segment XYXY.