Notes by Lex Toumbourou

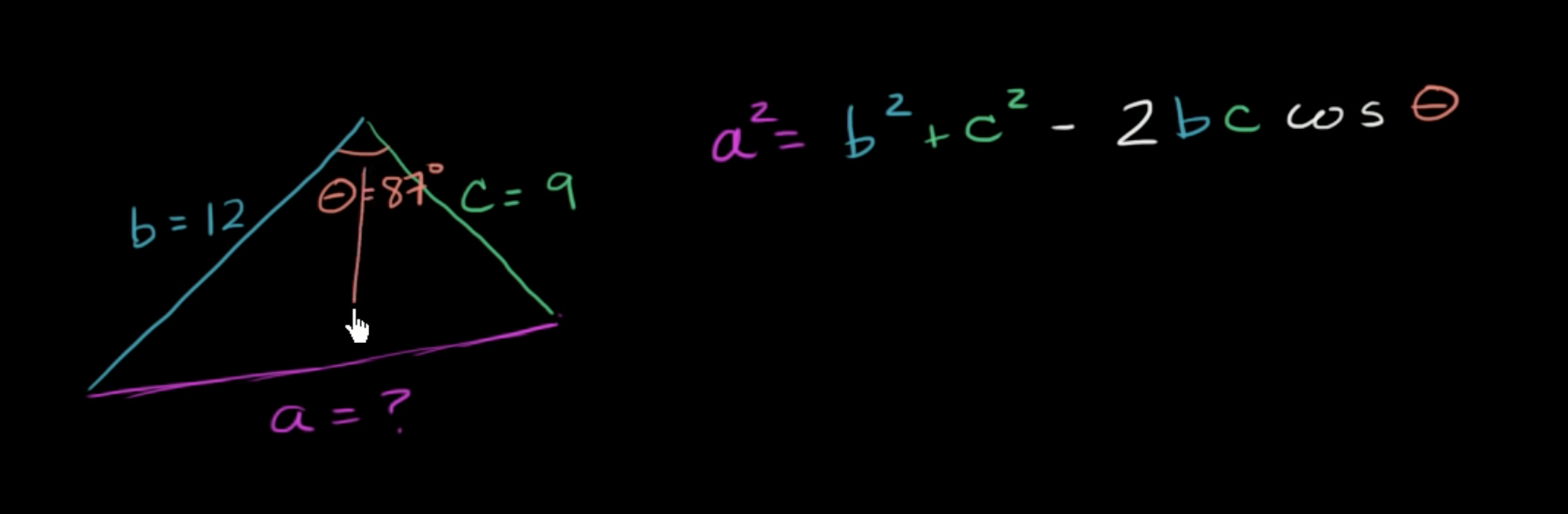
These are notes from the Khan Academy video series on Law of Cosines.

Solving for a side with the law of cosines

Given a triangle with sides A, B, and C and angle AB, if you know the length of A and B and angle AB, how can you calculate C?

If the triangle is a right-angle triangle, we can solve a missing side using Pythagoras Theorem:

$C^2 = B^2 + A^2$

For any triangle, we can use the law of cosines:

$C^2 = B^2 + A^2 - 2AB \cdot \cos(\theta)$

This expression makes sense because $\cos(90°) = 0$ . For a right-angle triangle, you can simply ignore the $-2AB \cdot \cos(\theta)$ component.

Solving for an angle with the law of cosines

If the angle is unknown, we can rewrite the expression as follows:

$cos(C) = \frac{a^2 + b^2 - c^2}{2ab}$

or

$C = acos(\frac{a^2 + b^2 - c^2}{2ab})$

Proof of the law of cosines

One way to solve the problem using the law of cosines is to convert them into two right triangles.

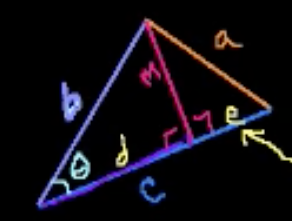
Then we can calculate the side $d$ knowing CAH: Cosine =Adjacent / Hypotenuse.

$\cos(\theta)=\frac{d}{b} \Rightarrow d = b\cos(\theta)$

We know that $e$ is $e = c - b\cos(\theta)$

Can calculate side $m$ since $m$ is opposite, we can use SOH: Sine = Opposite / Hypotenuse.

$\frac{m}{b}=\sin\theta \Rightarrow m=b \sin(\theta)$

Now we can use Pythagorean formula:

$a^2 = m^2 + e^2$ $a^2 = (b\sin(\theta))^2 + (c-b\cos(\theta))^2$

We can then multiply it out:

$b^2sin^2 \theta + c^2 - 2cb \cos\theta + b^2\cos^2 \theta$

We can then rearrange the expression:

$b^2 sin^2 \theta + b^2 \cos^2 \theta + c^2 - 2bc \cos \theta$

Which can be rewritten as:

$b^2(\sin^2\theta + \cos^2 \theta) + c^2 -2bc \cos \theta$

Since the first part of the expression is the product of $b^2$ and the Pythagorean identity, we can reduce it to $b^2$

$a^2 = b^2 + c^2 -2bc \cos \theta$

And that's the formula for the law of cosines!