Notes by Lex Toumbourou

Notes from Linear combinations, span, and basis vectors by 3Blue1Brown from the Essence of linear algebra series.

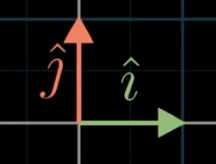
In the xy coordinate system there are 2 special vectors. One pointing to the right called $\hat{i}$: $\begin{bmatrix}1 \\ 0\end{bmatrix}$ or "the unit vector in the x direction" and one pointing up called $\hat{j}$: $\begin{bmatrix}1 \\ 0\end{bmatrix}$ or "the unit vector in the y direction".

We consider these the Basis Vectors of the XY coordinate system.

If you have a vector like $\begin{bmatrix}3 \\ -2\end{bmatrix}$, we can think of each component as a scalar that scales the Basis Vectors. The 3 scales the vector in the x-direction $\rightarrow$ and -2 in the y-direction $\uparrow$.

We can express the vector in terms of the basis vectors as: $(3)\hat{i} + (-2)\hat{j}$.

Note that we aren't limited to vectors $\begin{bmatrix}1 \\ 0\end{bmatrix}$ and $\begin{bmatrix}0 \\ 1\end{bmatrix}$ as Basis Vectors. You can choose any vectors as the basis vectors to give us an entirely new coordinate system. Any time we describe vectors numerically, it depends on an implicit basis vector choice.

For two vectors $\vec{v}$ and $\vec{w}$, we can imagine all the vectors you can reach by scaling each vector and adding the results. The answer is, in most cases, you can get to every possible vector.

If both vectors are on the same line, the result vector will all be limited to the same line.

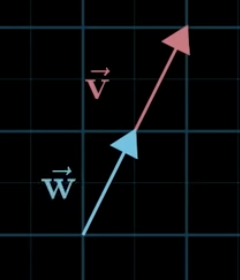
Also, any set of vectors to consider is both vectors have a magnitude of 0, which means they're stuck at the origin.

Anytime we're scaling two vectors and adding them, we call it a Linear Combination of vectors.

The Span of vectors $\vec{v}$ and $\vec{w}$ is the set of all possible linear combinations in this expression $a\vec{v} + b\vec{w}$ where $a$ and $b$ are real numbers.

When dealing with collections of vectors, we commonly represent them as points in space. Where the point sits at the tip of the vector.

When dealing with single vectors, we think of them as an arrow.

The span of most pairs of vectors is the entire space itself. When the vectors line up, the span is limited to just the line.

In 3d space, if you have two vectors pointing in a different direction, you can think of span as a flat sheet across 3d space.

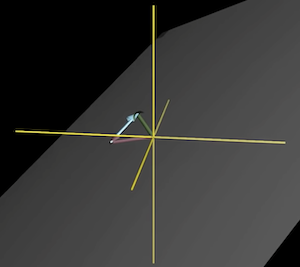
If you have three vectors, the span is the entire 3d space unless one vector shares a span with another.

Can think of the 3rd vector as moving the sheet created by the first 2 to move the rest of space.

We consider vectors Linearly Dependent when you have two vectors, and you can move one without changing the span. In other words, we can specify one of the vectors as a linear combination of the others.

Linear dependance: $\vec{u} = a\vec{v} + b\vec{w}$ for some values of a and b. Linear independance: $\vec{w} \neq a\vec{v}$ for all values of $a$

The technical definition of basis is a set of linearly independent vectors that span the entire space.