Notes by Lex Toumbourou

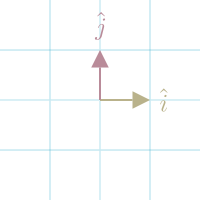
The set of Vectors that defines space is called the basis.

We refer to these vectors as basis vectors.

In 2d space, basis vectors are commonly defined as $\hat{i} = \begin{bmatrix}1 \\ 0\end{bmatrix}$ and $\hat{j} = \begin{bmatrix}0 \\ 1\end{bmatrix}$.

These particular vectors are called the standard basis vectors. We can think of them as 1 in the direction of X and 1 in the direction of Y.

We can think of all other vectors in the space as Linear Combinations of the basis vectors.

For example, if I have vector $\begin{bmatrix}10 \\ -7\end{bmatrix}$, we can treat each component as scalar (see Vector Scaling) for the basis vectors: $10\begin{bmatrix}1 \\ 0\end{bmatrix} + (-7)\begin{bmatrix}0 \\ 1\end{bmatrix}$.

We can choose any set of vectors as the basis vectors for space, giving us entirely new coordinate systems. However, they must meet the following criteria:

• They're linear independent. That means you cannot get one Vector by just scaling the other.
• They span the space. That means, by taking a linear combination of the two scaled vectors, you can return any vector.

Basis vectors don't have to be orthogonal to each other, but transformations become more challenging with a non-orthogonal basis.

3Blue1Brown (2016) Dye et al. (2018)

Backlinks

• Matrix Determinate