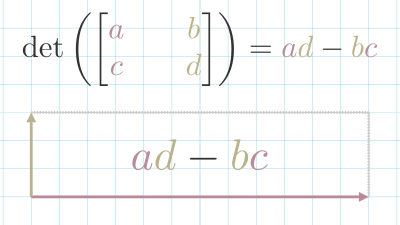Notes by Lex Toumbourou

The determinate of a Matrix Transformation refers to how much it scales space.

If we think of the standard Basis Vectors as the sides of a square, we can think of them as having an area of $1 \times 1 = 1$.

Then, if we transform them using matrix $\begin{bmatrix}2 && 0 \\ 0 && 4\end{bmatrix}$, the new area is $2 \times 4 = 8$. So we can say that the matrix has a determinant of 8.

$\det(\begin{bmatrix}2 && 0 \\ 0 && 4\end{bmatrix}) = 8$.

Once we know how much a transformation scales a single square, that tells us how any area in space would be scaled, since linear transformations "keep gridlines parallel and evenly spaced." [@3blue1brownVectorsChapter6Essence2016]

A determinate can be a fractional value, which reduces the size of space:

$\det\left(\begin{bmatrix}0.5 && 0.5 \\ 0.5 && 0.5\end{bmatrix}\right) = 0.5$

A determinate can even have a negative value, which means that the orientation of space is flipped.

$\det\left(\begin{bmatrix}-1 && 0 \\ 0 && -1\end{bmatrix}\right) = -1$

A Matrix Transformation was a determinate of 0, means that the transformation collapses space onto a single line. These types of matrices do not have a Matrix Inverse In 2d space, the Determinate can be calculated using this formula: $\det(\begin{bmatrix}{\color{red}{a}} && \color{green}{b} \\ \color{red}{c} && \color{green}{d}\end{bmatrix}) = {\color{red}{a}}{\color{green}{d}} - {\color{green}{b}}{\color{red}{c}}$.

The intuition for this comes when you set $b = 0$ and $c = 0$. In that case, the x and y-axis are scaled in a straight line. If you set either $b$ or $c$ to 0, the shape becomes a parallelogram. But the area is unchanged.

[@dyeMathematicsMachineLearning]

In 3d space, it becomes a lot more complex. We take the product of each element of the first row with the matrix that can be created excluding the current element's column and row.

$det\left(\begin{bmatrix}\color{red}{a_{11}} && \color{green}{a_{12}} && \color{blue}{a_{13}} \\ \color{red}{a_{21}} && \color{green}{a_{22}} && \color{blue}{a_{23}} \\ \color{red}{a_{31}} && \color{green}{a_{32}} && \color{blue}{a_{33}}\end{bmatrix}\right) = {\color{red}{a_{11}}} \ \det\left(\begin{bmatrix}\color{green}{a_{22}} && \color{blue}{a_{23}} \\ \color{green}{a_{32}} && \color{blue}{a_{33}}\end{bmatrix}\right) - {\color{green}{a_{12}}} \ \det\left(\begin{bmatrix}\color{red}{a_{21}} && \color{blue}{a_{23}} \\ \color{red}{a_{31}} && \color{blue}{a_{33}}\end{bmatrix}\right) + {\color{blue}{a_{13}}} \ \det\left(\begin{bmatrix}\color{red}{a_{21}} && \color{green}{a_{22}} \\ \color{red}{a_{31}} && \color{green}{a_{32}}\end{bmatrix}\right)$

[@khanacademylab3x3Determinant]

Backlinks

• Cardinality