Notes by Lex Toumbourou

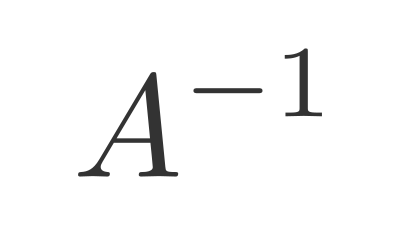
The inverse of a Matrix Transformation is a matrix that reverses the transformation.

For example, if our matrix transform did a 90° anticlockwise rotation, the inverse matrix would do a 90° clockwise rotation.

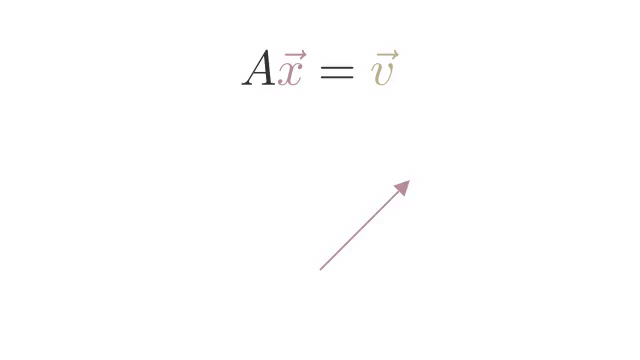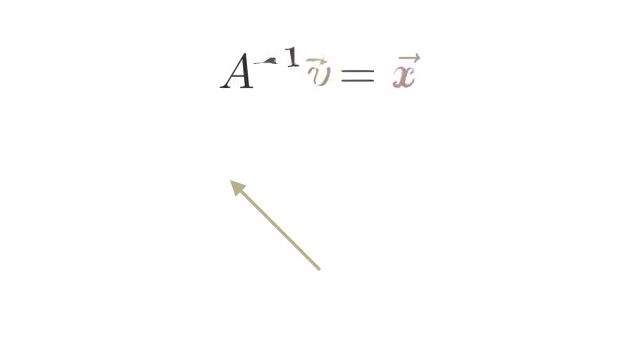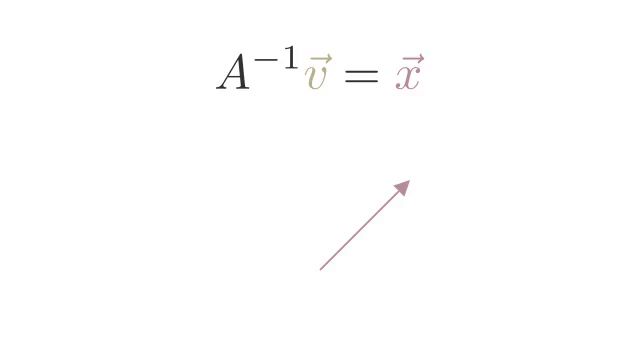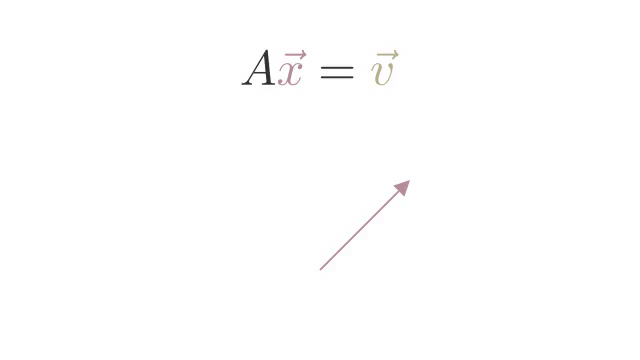
We represent the inverse of a matrix $A$ as $A^{-1}$.

When you multiply a matrix by its inverse, you get the Identity Matrix back: $A \cdot A^{-1} = I$

It's the equivalent of the reciprocal of a number in scalar math, ie $10 * \frac{1}{10} = 1$ or $10 \cdot 10^{-1} = 1$

For a $2 \times 2$ matrix, we calculate the inverse as follows:

$\begin{bmatrix}a & b \\ c & d\end{bmatrix}^{-1} = \frac{1}{ad-bc} \begin{bmatrix}d & -b \\ -c & a\end{bmatrix}$

For example:

$\begin{bmatrix}1 & 3 \\ 2 & 4\end{bmatrix}^{-1} = \frac{1}{1 \times 4 - 3 \times 2} \begin{bmatrix}4 & -3 \\ -2 & 1\end{bmatrix} = -\frac{1}{2} \begin{bmatrix}4 & -3 \\ -2 & 1\end{bmatrix} = \begin{bmatrix}-2 & 1.5 \\ 1 & -0.5\end{bmatrix}$

We can do a matrix multiplication to confirm the identity matrix is returned:

$\begin{bmatrix}1 & 3 \\ 2 & 4 \end{bmatrix} \begin{bmatrix}-2 & 1.5 \\ 1 & -0.5\end{bmatrix} = \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}$

We can also use the np.linalg.inv method in Numpy to find the inverse.

import numpy as np

m = np.array([[1, 3], [2, 4]])

m_inv = np.linalg.inv(m); m_inv

array([[-2. ,  1.5],
       [ 1. , -0.5]])

m @ m_inv

array([[1., 0.],
       [0., 1.]])

The $ad-bc$ part of the expression is the Matrix Determinate.

For a larger matrix, we can use Gaussian Elimination to invert a matrix.

[@dyeMathematicsMachineLearning]

A matrix with a determinate of 0: $|A| = 0$ is referred to as a Singular Matrix and has no inverse.

We can only calculate the inverse of a square matrix.

[@khanacademylabIntroMatrixInverses]

Backlinks

• Changing Basis
• Matrix Determinate