Changing Basis
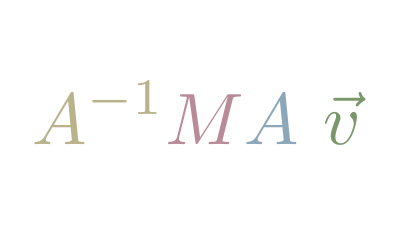
The use of coordinates to define vectors implies an agreement about which Basis Vectors we use. In 2d space, we commonly use the standard basis vectors:
, .
However, we are technically not limited to just the standard basis vectors: we can use any set of vectors to describe a coordinate system. Perhaps we encounter an Alien whose coordinate system uses these basis vectors:
, .
If the Alien describes a vector, say , in their coordinate system, we'd have first to translate it to our system.
We can translate back into our system by creating a matrix which uses the Alien basis vectors as the columns:
We can think of that as a Matrix Transformation that scales basis vector by and by .
We can convert a vector described in our coordinate system to the Alien using the Matrix Inverse of our Alien's basis vector matrix:
If we wish to perform a transformation described in our Basis, for example, a rotational transformation on an alternate basis, we can follow these steps:
- Convert the vector into our Basis by applying our friend's transformation matrix.
- Perform the translation.
- Convert the vector back into our friend's Basis by applying the inverse of the transformation.
In notation, if we have vector described in our friend's Basis , we can apply Matrix Transformation , described in our Basis, as follows: