Matrix Transformation
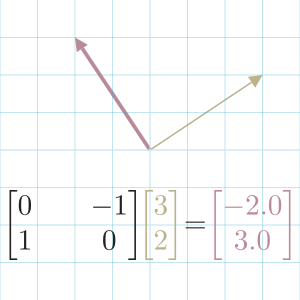
We can think of a matrix as a transformation of a Vector or all vectors in space.
When we take the product of a matrix and a vector, we are transforming the vector.
A transformation is another word for a function: it takes in some inputs (a vector) and returns some output (a transformed vector).
For example, we can rotate a vector [xy] some angle θ about the origin using a Rotational Matrix.
[x*y*]=[cosθsinθ−sinθcosθ][xy]
In this example, we perform a 90° rotation of vector [22].
To describe a transformation as a matrix, we only need to record where the Basis Vectors land as columns of a new matrix: [abcd]
For example, a Shear Transformation keeps the ˆi basis vector fixed, and slants the ˆj basis vector. We can record that as: [1102]
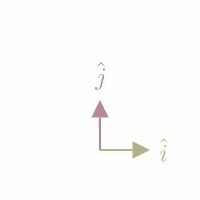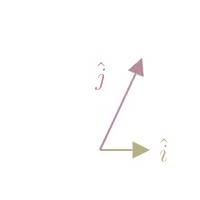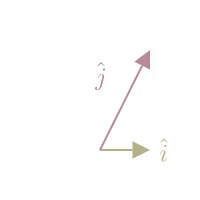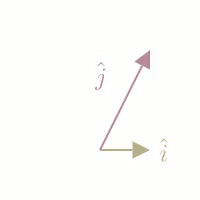
A matrix transformation is always linear in that it keeps all gridlines in space are parallel and evenly spaced.
[@3blue1brownVectorsChapter3Essence2016]
[@dyeMathematicsMachineLearning]
Image processing is a use case for matrix transformations.
Since we represent an image as a m x n grid of pixels, we can treat the position of each pixel as a vector, then perform a transform of each position vector to transform the entire image.
In this example, I rotate an image using the rotational matrix above.
There's some additional code required:
- Create a new matrix that's the maximum possible width and height.
- Convert each position into a vector.
- Convert each position vector, so it's a distance from the center, not top-left.
- Rotate each position.
- Revert convert using a new image size.
image = load_train_image(12)
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(14, 8))
ax1.imshow(rotate_image(image, 0), cmap='gray_r')
ax2.imshow(rotate_image(image, 90), cmap='gray_r')
ax3.imshow(rotate_image(image, 45), cmap='gray_r')
ax1.title.set_text('0° rotation')
ax2.title.set_text('90° rotation')
ax3.title.set_text('45° rotation')
plt.show()
Note that we end up with some empty pixels in a 45° rotation. These occur because some of the transformed coordinates are floating-point numbers. When they get rounded into integer positions, some of the pixels get excluded. There are many strategies to deal with this, but that's for another article.
[@agrawalRotatingImage]