Sigmoid Function

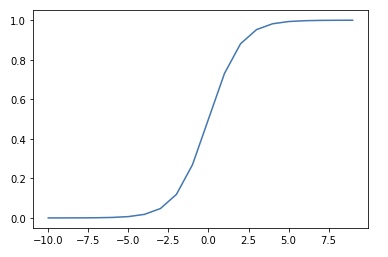
The Sigmoid function, also known as the Logistic Function, squeezes numbers into a probability-like range between 0 and 1.¹ Used in Binary Classification model architectures to compute loss on discrete labels, that is, labels that are either 1 or 0 (hotdog or not hotdog). The equation is:

$S(x) = \frac{1}{1 + e^{-x}}$

Intuitively, when x is infinity ($e^{-\infty}=0$), the Sigmoid becomes $\frac{1}{1}$ and when x is -infinity ($e^{\infty} = \infty$) the Sigmoid becomes $\frac{1}{inf}$. That means the model is incentivised to output values as high as possible in a positive case, and low for the negative case.

(Fox and Guestrin, 2016)

It is named Sigmoid because of its S-like Function Shape. Its name combines the lowercase sigma character and the suffix -oid, which means similar to.

It can be described and plotted in Python, as follows:

import math, matplotlib.pyplot as plt

def sigmoid_function(x):
    return 1/(1+math.e**(-x))

inputs = list(range(-10, 10, 1))
labels = [sigmoid_function(i) for i in inputs]

fig,ax = plt.subplots(figsize=(6,4))
ax.plot(inputs,labels)
plt.show()