Week 10 - Boolean Algebra B
5.201 Logic gates
- Logic Gate
- Implementation of a boolean operation.
- Basic element of an implementation of a Circuit.
-
- Most basic logic circuits:
- OR gates
- AND gates
- NOT gates
- All Boolean functions can be written in terms of these 3 logic operations.
-
- Produces HIGH output (value 1) when all inputs are HIGH otherwise, output is LOW (value 0).
- For a 2-input gate, AND gate is represented by electrical notation and truth table:
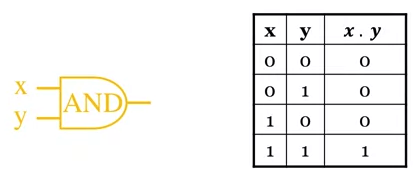
- The AND operations is written as or
- Produces HIGH output (value 1) when any of 2 inputs if HIGH, otherwise, output is LOW (value 0).
- For a 2-input gate, OR gate is represented by electrical notation and truth table:

- The OR operation is written as
- Produces opposite of the input.
- Also known as NOT gate.
- When input is LOW (0), output is HIGH (1) and vice versa.
- The inverter gate is represented by the following electrical notation and truth table:

- Not operation is written as
- Other gates:
- You can combine the basic gates to create 4 additional gates:
- True only when values of inputs differ

-
- AND Gate followed by an inverter.

- Equivalent to not AND
- AND Gate followed by an inverter.
-
- Equivalent to "not OR"
- OR Gate followed by an inverter.

-
- Equivalent to not XOR.

- Equivalent to not XOR.
- Multiple input gates
- AND, OR, XOR and XNOR operations are all commutative and associative
- They can be extended to more than 2 inputs.
- For example:
- The XNOR Gate can be applied to 3 inputs:

- NAND and NOR operations are both commutative but not associative.
- Extending number of inputs is less obvious here.
- When writing cascaded NAND and NOR operations, must use correct parentheses.
- The XNOR Gate can be applied to 3 inputs:
- Representing De Morgan's laws
- Theorem 1
- Complement of the product of variables, is equal to the sum of the complements of variables.
-

- Theorem 2
- Complment of the sum of variables, is equal to the product of the compliment of variables
-

- Most basic logic circuits:
5.203 Combinational circuits
- Outlines
- Definition of a circuit
- Building a circuit from a function
- Writing Boolean expressions from a circuit
- Building a circuit to model a problem
- Definition of a circuit
- Combination Circuits (aka logic networks)
- combination of Logic Gates designed to model Boolean functions.
- circuit that implements a Boolean function.
- logic values assigned to output signals is a Boolean function of current config of input signals.
- Combination Circuits (aka logic networks)
- Building a circuit from a function
- Given a Boolean function, we can implement a logic circuit representing all states of the function.
- Want to minimise the # of gates used to minimise the cost of the circuit.
- We can implement Boolean functions in different ways.
- Consider Boolean function :
- can be represented by this circuit:

- Writing a Boolean expression from a circuit
- Given a logic network, we can work out its corresponding Boolean function:
-
- label all gate outputs that are a function of the input variables.
-
- express the Boolean functions for each gate in the first level.
-
- repeat the process until all the outputs of the circuit are written as Boolean expressions.
-
- Example
-
- Label input of the circuit with symbols
-
- Express boolean functions for first level.
-
- Repeat for 2nd and third levels.
-
- Given a logic network, we can work out its corresponding Boolean function:
- Building a circuit to model a problem
- Combinational circuits are useful for desiging systems to solve specific problems, like addition, multiplication, decoders and multiplexers.
- Steps for building combinational circuit are:
-
- labelling the inputs and outsput using variables.
-
- modelling the problem as a Boolean expression
-
- replacing each operation by the equivalent logic gate.
-
- Building an adder circuit
- Consider building an adder for 2 one-digit binary bits x and y.
- From the truth table of this Boolean function, we know that:
- Can be designed as a half adder

- Half adder has limitations:
- no provision for carry input.
- circuit is not useful for multi-bit additions.
- Building a full adder circuit
- To overcome its limitations, transform half adder into a full adder by including gates for processing the carry bit.
- sum = x y carry in
- carry out = xy + carry in. (x y)

- 2 Boolean expression can be designed in as follows:

- We can hide some of the comlexity of a circuit by using a box diagram as a simple abstraction representing just the inputs and outputs.
5.205 Simplification of circuits
- Outline
- Benefits of simplification and Algebraic simplification
- Show how Boolean Algebra Theorem or rules can be used to represent and simplify Boolean functions.
- Introduce Karnaugh Map of Boolean functions.
- Benefits of simplification and Algebraic simplification
- Benefits of simplification
- We know that every function can be written in Sum-of-Products Form
- Not necessarily optimal in terms of number of gates and depth of circuit.
- Why circuits must be simplified:
- Reduces global cost of circuits, by reducing number of logic gates used
- Might reduce time computation cost of circuits
- Allows more circuits to be fitted on same chip
- We know that every function can be written in Sum-of-Products Form
-
Algebraic simplification
- Based on the use of Boolean algebra theorems to represent and simplify the behaviour of Boolean Functions.
- To produce a sum-of-product expression, need to use one or all of following theorems:
- De Morgan's laws and involution
- Distributive laws
- Commutative, idempotent and complement laws
- Absorption law
-
Example
- Consider this Boolean expression:
- Using De Morgan's laws and involution:
- $$
\begin{align} E &= (xy)'' + z')((x' + =z)'+(y' + z')') \ &= (xy + z')((x'' . z') +y'' . z'') \ &= (xy + z')(xz' + yz) \end{align}
$ * Can be further simplified using **distributive** laws: E = xyxz' + xyyz + z'xz' + z'yz$ * Using commutative, idempotent and complement laws: * Using absorption law:
-
Example 2
- Consider full adder circuit from last week.
- Using truth table, we can build a sum-of-products form for the 2 functions:

- Karnaugh Maps
- A Karnaugh map (or K-Map) is a graphic representation of a Boolean function and differs from a truth table.
- It can be used for expressions with 2, 3, 4 or 5 variables.
- A K-Map is shown in an array of cells and cells differing by only one variable are adjacent.
- The number of cells in a K-Map is the total number of possible input variable combinations which is .

- Example
- Consider the Boolean function described in the truth table shown here:
- We have 3 variables, we need a 3-input K-Map for which we identify all the 1's first.
- Group each 1 value with the maximum possible number of adjacent 1's to form a rectangle, power of 2 long (1, 2, 4, 8)
- Then, write a term for this rectangle.
- In this case, it's the minimised expression of is:


- Consider the Boolean function described in the truth table shown here:
- A Karnaugh map (or K-Map) is a graphic representation of a Boolean function and differs from a truth table.
5.211 Domino logic gates simulation
- Learn about logic gates and how to represent them using dominoes.
- Logic gates are basic element of electronic circuitts, implementing a boolean operation.
- Computers are made of billions of these tiny electrical components. Depending on characteritics of eahc gate, logic gates take information coming in and output the processed information accordingly.
- It is difficult to visualise this rpcoess in computers as the info they get is in electrical signals. The signal can either be on or off. It depends on the voltage registered.
- Can break down complex system using dominoes.
- The info is dicated by whether a chain of dominoes is falling or not, representing high voltage and low voltage respectively.
- The next exercise wil simulate different types of logic
5.208 Summative quiz
Questions I did not understand
Which of the following expressions is a sum-of-products form of the Boolean expression:
Why is it 3 variables in each product term?
By distributivity: By identity: By distributivity: By idempotent law:
Find the simplification of the expression represented by the following K-map.

I accidentally got it right.
Assignment
Question
Given the Boolean function , write the sum-of-products expansion of where all the variables are used.
Answer
- Distributive law:
- Identity law:
- Complement law:
- Distributive law:
- Idempotent law:
Problem Sheet
- What is the output for each of the logic circuits?

How can I know the output if I don't know what the input is? Maybe some kind of algebraic reduction?
Looks like my initial answer was correct, I just didn't include the NOT part of the circuit after
- Write down the truth table for the output Q of the following circuit.

| A | B | (A + B) | (A + B) | (A + B) + B | ( (A + B) + B) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
- Simplify each Boolean expression to one of the following expressions:
- -- DeMorgan's law
- A.B -- involution theorem
- -- distributivity
- (A + 0) + B -- complements
- A + B -- identity
- -- Distributivity
- -- Involution
- -- Distributivity
- -- Commutativity
- 0 + 0
- 0
- Use the laws of Boolean Algebra to simplify the boolean expression:
- -- identity law
- -- Distributive law
- -- Distributibe law
- -- Complements
- a + b
- Use a truth table to prove that
| a | b | a + b | |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
3. Simplified circuit is just $a + b$
- What is the output of the following logical circuit?
- Use the truth table to prove De Morgan's laws:
| a | b | ab | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| a | b | a + b | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
- Use the laws of boolean algebra to simplify:
-- Complement -- Idempotent -- Distributive law
-- De Morgan's law -- Distributive law -- Complement -- Idemptotent -- Idemptotent -- Distributive -- Complement -- Complement -- Identity -- Identity -- Idempotent
- Use laws of boolean algebra to simplify the boolean expression
-- idempotent laws -- commutative laws
Even the answers don't make sense here.
- Prove that in a boolean algebra You are required to explain your answer by making a reference to a boolean algebra axioms (laws)
a.a = a a = a -- Idempotent laws.
The answer should be:
\begin{align} a &= a.1 \\ &= a . (a + \overline{a}) \\ &= a . a + a . \overline{a} \\ &= a^2 + 0 \\ &= a^2 \\ \end{align}
- The following diagram shows a circuit with three inputs and two outputs, and

- List the logic gates used
3 OR gates and 2 AND gates
- Describe each output u and v as a Boolean expression in terms of x, y and z
- Derive the Boolean expression for the following logic circuit shown below

- Write down a boolean expression for the following input/output behaviour
| x | y | z | u |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
-
Write a boolean expression for input/output behaviour.
-
Construct the corresponding circuit of the above expression using not-games, and-gates and or-gates only

