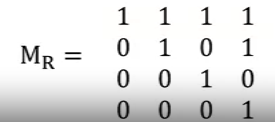Week 17 - Relations A

Lesson 9.1 Understanding the concept of relations

9.101 Introduction

• Relationships between elements of sets occur in many contexts.
• We deal with relationships in a daily basis:
  • A relationship between a person and a relative.
  • A relationship between an employee and their salary.
  • A relationship between a business and its telephone number.
  • A relationship between a computer language and a valid statement in this language will often arise in computer science.
• In maths, we study relationships like:
  • the relation between a positive integer and one it divides.
  • relation between a real number and one that is larger than it.
  • relation between a business and its telephone number.
  • relation between a computer language and a valid statement
  • relation between a real number x and the value f(x) where f is a function, and so on.
• Relations in maths
  • We can define relationship between elements of 2 sets
  • We can also define the relationship between 2 elements of a set.

9.103 Definition of a relation: relation versus function

• Relation
  • A relation can be defined between elements of set A and elements of another set B.
  • Can also be defined between elements of the same set.
  • We use the letter $R$ to refer to relation.
  • Let $A$ and $B$ be two sets.
  • Let $R$ be a relation linking elements of set $A$ to elements of set $B$.
  • Let $x \in A$ and $y \in B$
    • We say that $x$ is related to $y$ with respect to relation $R$ and we write $x \ R \ y$
  • A relation can also be between elements of the same set.
  • A relation is a link between two elements of a set
    • For example
      • A person x is a SON OF' a person y.
      • SON OF is a relation that links x to y
    • Usually use the letter $R$ to refer to a relation:
      • In this case $R$ = 'SON OF'
      • If $x$ is SON OF $y$ we write $x \ R \ y$
      • If $y$ is NOT a SON OF $x$ we write $y \ \not R \ x$
  • A relation can be defined as a link or connection between elements of set A to set B.
  • Example
    • A is the set of students in a Comp Science class
      • $A = \{Sofia, Samir, Sarah\}$
    • B is the courses the department offers
      • $B = \{Maths, Java, Databases, Art\}$
    • Let $R$ be a relation linking students in set $A$ to classes they are enrolled in: A student is related to the course if the student is enrolled in the course.
    • Examples:
      • Sofia is enrolled in Math and Java
      • Samir is enrolled in Java and Databases
      • Sarah is enrolled in Math and Art
      • Sofia is not enrolled in Art
    • Notations:
      • Sofia $R$ Maths
      • Sofia $R$ Java
      • Samir $R$ Java
      • Samir $R$ Databases
      • Sarah $R$ Maths
      • Sarah $R$ Art
      • Sofia $\not R$ Art
• Cartesian product
  • Let $A$ and $B$ be 2 sets.
  • The Cartesian product A x B is defined by a set of pairs (x, y) such that $x \in A$ and $y \in B$
    • $A \ x \ B = \{(x, y): x \in A \text{ and } y \in B \}$
  • For example:
    • $A = \{ a_1, a_2 \}$ and $B = \{b_1, b_2, b_3\}$
    • $A \ x \ B = \{(a_1, b_1), (a_1, b_2), (a_1, b_3), (a_2, b_1), (a_2, b_2), (a_2, b_3)\}$
• Definition of relation
  • Let $A$ and $B$ be two sets.
  • A binary relation from A to B is a subset of a Cartesian product $A \ x \ B$
    • $R \subseteq A \ x \ B$ means $R$ is a set of ordered pairs of the form (x, y) where $x \in A$ and $y \in B$.
    • $(x, y) \in R$ means $x \ R \ y$ (x is related to y)
  • For example:
    • $A = \{a, b, c\}$ and $B = \{1, 2, 3\}$
    • The following is a relation defined from A to B:
      • $R = \{(a, 1), (b, 2), (c, 3)\}$
      • This means that: $a\ R \ 1$, $b \ R \ 2$ and $c \ R \ 3$
• Relations on a set
  • When A = B
  • A relation R on the set A is a relation from A to A
    • $R \subseteq A \ x \ A$
  • We will be studying relations of this type.
  • Example
    • A = {1, 2, 3, 4}
    • Let R be a relation on the set A:
      • $x, y \in A$, $x \ R \ y$ if and only if $x < y$
    • We have 1 R 2, 1 R 3, 1 R 4, 2 R 3, 2 R4, 3 R 4
    • $R = \{(1,2), (1,3),(1,4), (2, 3), (2, 4), (3, 4)\}$

9.105 Matrix and graph representatins of a relation

• Relations using matrices
  • Given a relation R from a set A to set B.
  • List the elements of sets A and B in a particular order
  • Let $n_a = |A|$ and $n_b = |B|$
  • The matrix of R is an $n_a \ \text{x} \ n_b$ matrix.
    • $M_r = [m_{ij}] n_a \ x \ n_b$
  • In matrix store a 1 if $(a_i, b_j) \in R$ otherwise, 0
• Example 1
  • Let A = {Sofia, Samir, Sarah}
  • Let B = {CS100, CS101, CS102, CS103}
  • Consider the relation of who is enrolled in which class
  • R = { (a,b) | person a is enrolled in course b }

	CS100	CS101	CS102
Sofia	x	x
Samir		x	x
Sarah	x		x

$M_r = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{bmatrix}$

• Example 2
  • Let A = { 1, 2, 3, 4, 5 }
  • Consider a relation: $< (x, y) \in R \text{ if and only if } x < y$
  • Every element is not related to itself (hence the diagonal 0s).

$M_r = \begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}$

• Example 3
  • Let A = { 1, 2, 3, 4, 5 }
  • Consider a relation : $\leq (x, y) \in R$ if and only if $x \leq y$
  • Note the diagonal is all 1s.

$M_r = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}$

• Combining relations
  • Union
    • The Union of 2 relations is a new set that contains all of the pairs of elements that are in at least one of the two relations.
    • The union is written as $R \ U \ S$ or "R or S".
    • $R \ U \ S$ = { $(a, b): (a, b) \in R$ or $(a, b) \in S$ }
  • Intersection
    • The intersection of 2 relations is a new set that contains all of the pairs that are in both sets.
    • The intersection is written as $R \cap S$ or "R and S"
    • $R \cap S$ = { $(a, b): (a, b) \in R$ and $(a, b) \in S$ }
  • Combining relations: via Boolean operators
    • Let $M_{R} = \begin{bmatrix}1 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \\ M_{s} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}$
    • Join $M_{R \cup S} = M_R \vee M_S = \begin{bmatrix}1 & 0 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 0\end{bmatrix}$
    • Meet $M_{R \cap S} = M_R \land M_S = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$
• Representing relations using directed graphs
  • When a relation is defined on a set, we can represent with a digraph.
  • Building the digraph
    • First, the elements of A are written down,
    • When $(a, b) \in R$ arrows are drawn from a to b.
  • Example 1
    • A = { 1, 2,3 ,4}
    • Let R be relation on A defined as follows:
      • R = { $(x, y)$ | x divides y}
      • R can be represented by this digraph
      • 
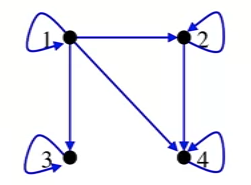
        • Each value divides itself, hence the loop at each vertex.
        • One divides all other elements, so it has a link to each elements.
        • 2 only divides into 4
        • So on...
  • Example 2
    • Let A = { 1, 2, 3, 4, 5 }
    • Consider relation: $\leq (x, y) \in R$ if and only if $x \leq y$
    • 
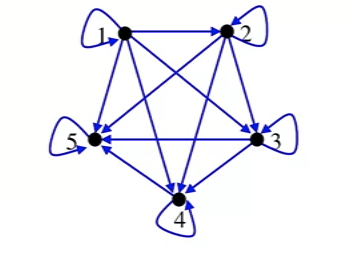
      • Each element is equal to itself.
      • One is less than or equal to all elements.
      • 5 is greater than all elements except itself.
      • So on.

9.107 The properties of a relation: reflexive, symmetric and anti-symmetric

• Reflexivity
  • A relation R in a set S is said to be reflexive if and only if $x \ R \ x$, $\forall x \in S$
    • Or, for all x in the set, if the pairs (x, x) is in the relation, then it's reflexive.
  • Example 1 (reflexive example)
    • Let R be a relation of elements in Z:
      • $R = \{ (a, b) \in Z^2 | a \leq b \}$
    • For all x elements of Z, we have $x \leq x$, hence $x \ R \ x$
    • This implies that R is reflexive.
  • Example 2 (non-reflexive)
    • $R = \{ (a, b) \in Z^2 | a \lt b \}$
  • Digraph of reflexive relation
    • Every element will have a loop.
    • In this example, S = {1, 2, 3, 4} and R is a relation of elements S $R = \{ (a, b) \in S^2 | a \leq b \}$
  • Matrix of reflexive relation
    • Same example as above.
    • Note that all the values in the diagonal are 1.
• Definition of Symmetry
  • A relation is said to be symmetric if and only if:
    • $\forall a, b \in S$, if $a \ R \ b$ then $b \ R \ a$.
  • Proof: let $a, b \in Z$ with $a \ R \ b$:
    • a mod 2 = b mod 2
    • b mod 2 = a mod 2
    • b R a
  • R is symmetric
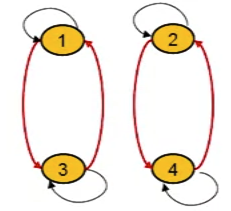
• Diagram of a symmetric relation
• Example
  • Let S = {1, 2, 3, 4} and R be relation of elements in S
    • R = { (a,b) \in S^2 | a mod 2 = b mod 2 }
• Matrix of symmetric relation
  • Example
    • Let S = {1, 2, 3, 4} and let R be relation of elements in S
      • R = { (a, b) \in S^2 | a mod 2 = b mod 2 }
    • $M_R = \begin{bmatrix}1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1\end{bmatrix}$
• Definition of anti-symmetric
  • A relation R on a set S is said to be anti-symmetric if and only if $\forall a, b \in S$, if $a \ R \ b$ and $b \ R \ a$ then $a = b$
    • In other words, no 2 diff elements are related both ways.
  • Examples
    • Let R be a relation on elements in Z:
      • $R = \{ (a, b) \in Z^2 | a \leq b \}$
    • Let $a, b \in Z$, $a \ R \ b$ and $b \ R \ a$
      • $a \leq b$ and $b \leq a$
      • $a = b$
    • R is anti-symmetric
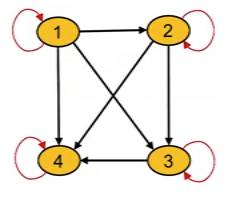
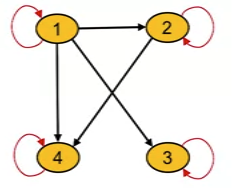
• Digraph of anti-symmetric relation
  • Digraph contains no parallel edges between any 2 different vertices.
  • Example
    • Let S = {1, 2, 3, 4} and R be relation on elements in S
      • $R = \{ (a, b) \in S^2 | \text{ a divides b } \}$
• Matrix of an anti-symmetric relation
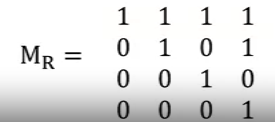
• Exercise
• Let R be the relation defined by the Matrix M_r
  • $M_r = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}$
• Is R reflexive? Symmetric? Anti-symmetric?
• Clearly R is not reflexive: $m_{1,1} = 0$
• It is not symmetric because $m_{2,1}=1, m_{1, 2}=0$
• However, it is anti-symmetric.

9.109 Relation properties: transitivity

• Definition of transitivty
  • A relation $R$ on a set S is called transitive if and only if:
    • $\forall a, b, c \in S$, if ($a \ R \ b$ and $b \ R \ c$) then $a \ R \ c$
• Examples of transitive relations
  • $R = \{ (x , y) \in N^{2} | x \leq y \}$
    • It is transitive as $\forall x, y, z \in \mathbf{N}$ if $x \leq y$ and $y \leq z$ then $x \leq z$
  • R = { (a, b) | a is an ancestor of b }
    • It is transitive because if a is an acestory of b and b is an ancestor of c, then a is an ancestor of c.
• Example of non-transitive relations
  • R = { (2, 3), (3, 2), (2, 2) }
    • It is not transitive because 3 R 2 and 2 R 3 but 3 \not R 3
  • 
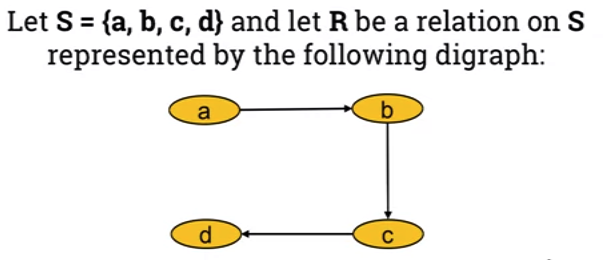
    • Not transitive as:
      • $a \ R \ c$ and $b \ R \ c$, however $a \ \not R \ c$
      • Also: $b \ R \ c$ and $c \ R \ d$ however $b \ \not R \ d$
  • What edges need to be added to make it transitive?
    • 
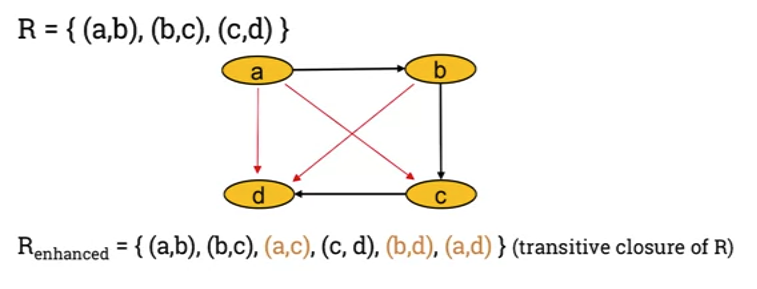
      • The result enhanced relation is called the "transitive closure of the original relation"