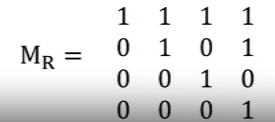Lesson 9.1 Understanding the concept of relations
9.101 Introduction
- Relationships between elements of sets occur in many contexts.
- We deal with relationships in a daily basis:
- A relationship between a person and a relative.
- A relationship between an employee and their salary.
- A relationship between a business and its telephone number.
- A relationship between a computer language and a valid statement in this language will often arise in computer science.
- In maths, we study relationships like:
- the relation between a positive integer and one it divides.
- relation between a real number and one that is larger than it.
- relation between a business and its telephone number.
- relation between a computer language and a valid statement
- relation between a real number x and the value f(x) where f is a function, and so on.
- Relations in maths
- We can define relationship between elements of 2 sets
- We can also define the relationship between 2 elements of a set.
9.103 Definition of a relation: relation versus function
- Relation
- A relation can be defined between elements of set A and elements of another set B.
- Can also be defined between elements of the same set.
- We use the letter R to refer to relation.
- Let A and B be two sets.
- Let R be a relation linking elements of set A to elements of set B.
- Let x∈A and y∈B
- We say that x is related to y with respect to relation R and we write x R y
- A relation can also be between elements of the same set.
- A relation is a link between two elements of a set
- For example
- A person x is a SON OF' a person y.
- SON OF is a relation that links x to y
- Usually use the letter R to refer to a relation:
- In this case R = 'SON OF'
- If x is SON OF y we write x R y
- If y is NOT a SON OF x we write y R x
- A relation can be defined as a link or connection between elements of set A to set B.
- Example
- A is the set of students in a Comp Science class
- A={Sofia,Samir,Sarah}
- B is the courses the department offers
- B={Maths,Java,Databases,Art}
- Let R be a relation linking students in set A to classes they are enrolled in: A student is related to the course if the student is enrolled in the course.
- Examples:
- Sofia is enrolled in Math and Java
- Samir is enrolled in Java and Databases
- Sarah is enrolled in Math and Art
- Sofia is not enrolled in Art
- Notations:
- Sofia R Maths
- Sofia R Java
- Samir R Java
- Samir R Databases
- Sarah R Maths
- Sarah R Art
- Sofia R Art
- Cartesian product
- Let A and B be 2 sets.
- The Cartesian product A x B is defined by a set of pairs (x, y) such that x∈A and y∈B
- A x B={(x,y):x∈A and y∈B}
- For example:
- A={a1,a2} and B={b1,b2,b3}
- A x B={(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3)}
- Definition of relation
- Let A and B be two sets.
- A binary relation from A to B is a subset of a Cartesian product A x B
- R⊆A x B means R is a set of ordered pairs of the form (x, y) where x∈A and y∈B.
- (x,y)∈R means x R y (x is related to y)
- For example:
- A={a,b,c} and B={1,2,3}
- The following is a relation defined from A to B:
- R={(a,1),(b,2),(c,3)}
- This means that: a R 1, b R 2 and c R 3
- Relations on a set
- When A = B
- A relation R on the set A is a relation from A to A
- R⊆A x A
- We will be studying relations of this type.
- Example
- A = {1, 2, 3, 4}
- Let R be a relation on the set A:
- x,y∈A, x R y if and only if x<y
- We have 1 R 2, 1 R 3, 1 R 4, 2 R 3, 2 R4, 3 R 4
- R={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
9.105 Matrix and graph representatins of a relation
- Relations using matrices
- Given a relation R from a set A to set B.
- List the elements of sets A and B in a particular order
- Let na=∣A∣ and nb=∣B∣
- The matrix of R is an na x nb matrix.
- Mr=[mij]na x nb
- In matrix store a 1 if (ai,bj)∈R otherwise, 0
- Example 1
- Let A = {Sofia, Samir, Sarah}
- Let B = {CS100, CS101, CS102, CS103}
- Consider the relation of who is enrolled in which class
- R = { (a,b) | person a is enrolled in course b }
|
CS100 |
CS101 |
CS102 |
| Sofia |
x |
x |
|
| Samir |
|
x |
x |
| Sarah |
x |
|
x |
Mr=⎣⎢⎡101110011⎦⎥⎤
- Example 2
- Let A = { 1, 2, 3, 4, 5 }
- Consider a relation: <(x,y)∈R if and only if x<y
- Every element is not related to itself (hence the diagonal 0s).
Mr=⎣⎢⎢⎢⎢⎢⎡0000010000110001110011110⎦⎥⎥⎥⎥⎥⎤
- Example 3
- Let A = { 1, 2, 3, 4, 5 }
- Consider a relation : ≤(x,y)∈R if and only if x≤y
- Note the diagonal is all 1s.
Mr=⎣⎢⎢⎢⎢⎢⎡1000011000111001111011111⎦⎥⎥⎥⎥⎥⎤
- Combining relations
- Union
- The Union of 2 relations is a new set that contains all of the pairs of elements that are in at least one of the two relations.
- The union is written as R U S or "R or S".
- R U S = { (a,b):(a,b)∈R or (a,b)∈S }
- Intersection
- The intersection of 2 relations is a new set that contains all of the pairs that are in both sets.
- The intersection is written as R∩S or "R and S"
- R∩S = { (a,b):(a,b)∈R and (a,b)∈S }
- Combining relations: via Boolean operators
- Let MR=⎣⎢⎡110001100⎦⎥⎤Ms=⎣⎢⎡101010110⎦⎥⎤
- Join MR∪S=MR∨MS=⎣⎢⎡111011110⎦⎥⎤
- Meet MR∩S=MR∧MS=⎣⎢⎡100000100⎦⎥⎤
- Representing relations using directed graphs
- When a relation is defined on a set, we can represent with a digraph.
- Building the digraph
- First, the elements of A are written down,
- When (a,b)∈R arrows are drawn from a to b.
- Example 1
- A = { 1, 2,3 ,4}
- Let R be relation on A defined as follows:
- R = { (x,y) | x divides y}
- R can be represented by this digraph
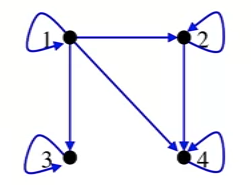
- Each value divides itself, hence the loop at each vertex.
- One divides all other elements, so it has a link to each elements.
- 2 only divides into 4
- So on...
- Example 2
- Let A = { 1, 2, 3, 4, 5 }
- Consider relation: ≤(x,y)∈R if and only if x≤y
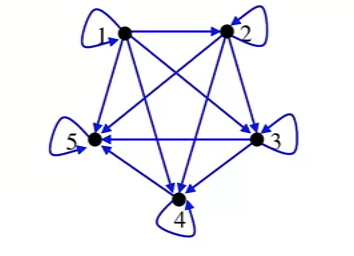
- Each element is equal to itself.
- One is less than or equal to all elements.
- 5 is greater than all elements except itself.
- So on.
9.107 The properties of a relation: reflexive, symmetric and anti-symmetric
- Reflexivity
- A relation R in a set S is said to be reflexive if and only if x R x, ∀x∈S
- Or, for all x in the set, if the pairs (x, x) is in the relation, then it's reflexive.
- Example 1 (reflexive example)
- Let R be a relation of elements in Z:
- R={(a,b)∈Z2∣a≤b}
- For all x elements of Z, we have x≤x, hence x R x
- This implies that R is reflexive.
- Example 2 (non-reflexive)
- R={(a,b)∈Z2∣a<b}
- Digraph of reflexive relation
- Every element will have a loop.
- In this example, S = {1, 2, 3, 4} and R is a relation of elements S R={(a,b)∈S2∣a≤b}
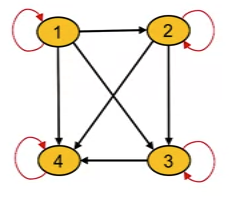
- Matrix of reflexive relation
- Same example as above.
- Note that all the values in the diagonal are 1.

- Definition of Symmetry
- A relation is said to be symmetric if and only if:
- ∀a,b∈S, if a R b then b R a.
- Proof: let a,b∈Z with a R b:
- a mod 2 = b mod 2
- b mod 2 = a mod 2
- b R a
- R is symmetric
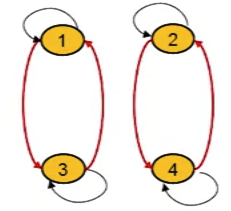
- Diagram of a symmetric relation
- Example
- Let S = {1, 2, 3, 4} and R be relation of elements in S
- R = { (a,b) \in S^2 | a mod 2 = b mod 2 }
- Matrix of symmetric relation
- Example
- Let S = {1, 2, 3, 4} and let R be relation of elements in S
- R = { (a, b) \in S^2 | a mod 2 = b mod 2 }
- MR=⎣⎢⎢⎢⎡1010010110100101⎦⎥⎥⎥⎤
- Definition of anti-symmetric
- A relation R on a set S is said to be anti-symmetric if and only if ∀a,b∈S, if a R b and b R a then a=b
- In other words, no 2 diff elements are related both ways.
- Examples
- Let R be a relation on elements in Z:
- R={(a,b)∈Z2∣a≤b}
- Let a,b∈Z, a R b and b R a
- a≤b and b≤a
- a=b
- R is anti-symmetric
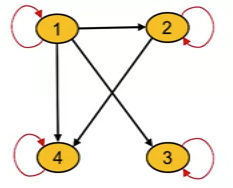
- Digraph of anti-symmetric relation
- Digraph contains no parallel edges between any 2 different vertices.
- Example
- Let S = {1, 2, 3, 4} and R be relation on elements in S
- R={(a,b)∈S2∣ a divides b }
- Matrix of an anti-symmetric relation
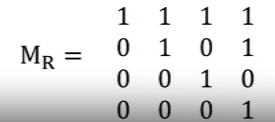
- Exercise
- Let R be the relation defined by the Matrix M_r
- Mr=⎣⎢⎡010010111⎦⎥⎤
- Is R reflexive? Symmetric? Anti-symmetric?
- Clearly R is not reflexive: m1,1=0
- It is not symmetric because m2,1=1,m1,2=0
- However, it is anti-symmetric.
9.109 Relation properties: transitivity
- Definition of transitivty
- A relation R on a set S is called transitive if and only if:
- ∀a,b,c∈S, if ($a \ R \ b$ and b R c) then a R c
- Examples of transitive relations
- R={(x,y)∈N2∣x≤y}
- It is transitive as ∀x,y,z∈N if x≤y and y≤z then x≤z
- R = { (a, b) | a is an ancestor of b }
- It is transitive because if a is an acestory of b and b is an ancestor of c, then a is an ancestor of c.
- Example of non-transitive relations
- R = { (2, 3), (3, 2), (2, 2) }
- It is not transitive because 3 R 2 and 2 R 3 but 3 \not R 3
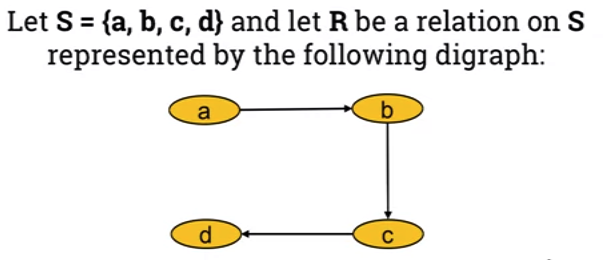
- Not transitive as:
- a R c and b R c, however a R c
- Also: b R c and c R d however b R d
- What edges need to be added to make it transitive?
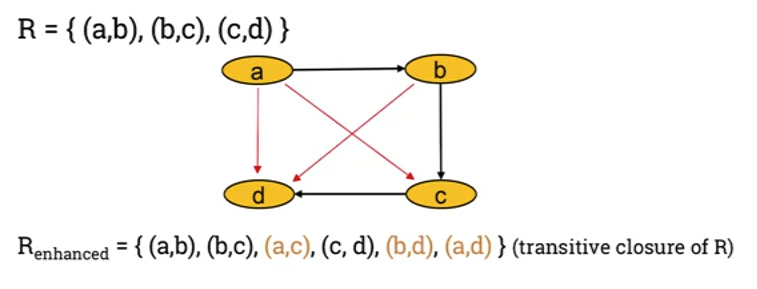
- The result enhanced relation is called the "transitive closure of the original relation"