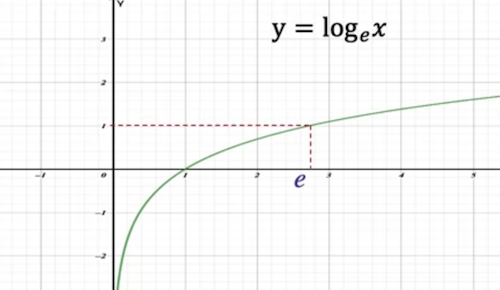Week 4 - Functions B
2.201 Function composition
-
- Given two functions f and g:
- Firstly we pass into to get
- Then we pass the function output into to get
-
Example of function composition:
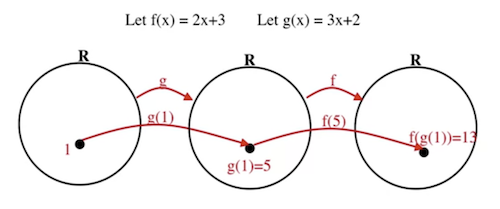
-
Function composition is not commutative
- Example:
- and
- Therefore,
- Given two functions f and g:
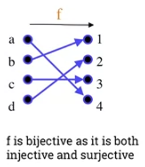
2.203 Bijective function
-
- A function is said to be bijective or invertible if and only if it is both injective and surjective.
- Examples:
-
is bijective as it is both injective and surjective.
 * is bijective as it isn't surjective
* is bijective as it isn't surjective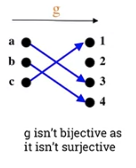 * isn't bijective as it isn't injective.
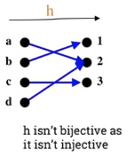
* isn't bijective as it isn't injective.
 * Show that the function: with is a bijective (invertible) function.
* Show that f is injective (one-to-one)
* Proof:
* Let , show that if then
*
* Show that f is surjective (onto)
* Proof:
* Let show that there exists such that
*
* Therefore, for every element in there exists which is such that
* Since we have shown that is both injective and surjective, we can infer that it is a bijective function.
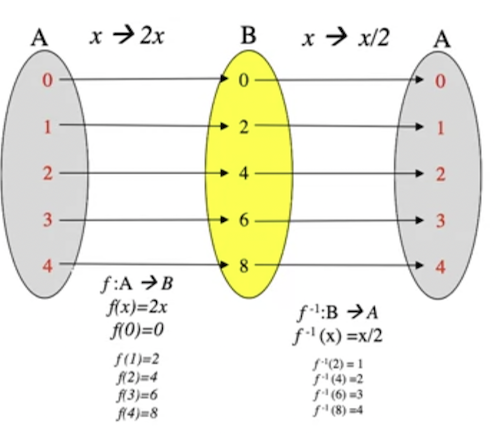
* Inverse Function
* Let
* If is bijective (invertible) then the inverse function, , exists and is defined as follows:
* What the inverse function really does is reverse the function .
* Example 1
* Show that the function: with is a bijective (invertible) function.
* Show that f is injective (one-to-one)
* Proof:
* Let , show that if then
*
* Show that f is surjective (onto)
* Proof:
* Let show that there exists such that
*
* Therefore, for every element in there exists which is such that
* Since we have shown that is both injective and surjective, we can infer that it is a bijective function.
* Inverse Function
* Let
* If is bijective (invertible) then the inverse function, , exists and is defined as follows:
* What the inverse function really does is reverse the function .
* Example 1
 * Example 2: Let
* Example 2: Let
-
 * Exercise: The following function find the inverse function,
* We know it's injective and surjective.
*
*
*
*
*
*
* A function f of its inverse is equal to the identity function:
*
*
*
*
*
* Plotting on a graph
* The curves of and are symmetric with respect to the straight line .
* Exercise: The following function find the inverse function,
* We know it's injective and surjective.
*
*
*
*
*
*
* A function f of its inverse is equal to the identity function:
*
*
*
*
*
* Plotting on a graph
* The curves of and are symmetric with respect to the straight line .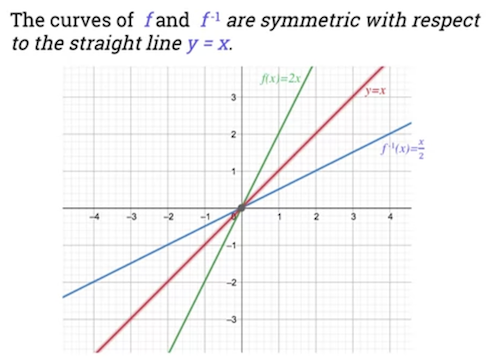
2.205 Logarithmic functions
-
- The variable is called the base.
- Defined by and where and .
-
Graphs:
-
First graph shows exponential growth where base > 1.
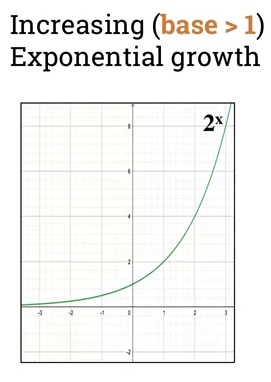
-
-
2nd graphs exponential decay where b < 1.
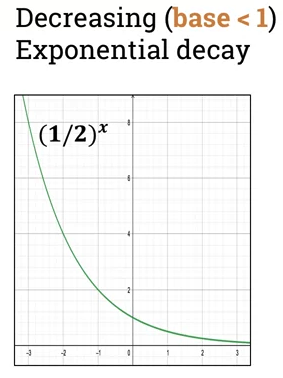
-
Properties of exponential function:
- where ($b > 0$ and ).
- Domain is set all real numbers: ;
- Range is all positive real numbers:
- The graph always passes through the point with coords
- if base is > 1, then function is increasing
- called "exponential growth"
- if base < 1, then function is decreasing
- called "exponential decay"
- it is Injective and Surjective, hence, it has an inverse function.
- Logarithmic Functions
- Logarithmic function with base b where b > 0 and is defined as follows:
- if and only if
- is inverse of exponential function .
- The exponent in the exponential becomes what the log is equal to.
- Laws of Logarithms
- Examples
- , so
- Since = 1,
-
Examples of a logarithmic function
- Can see function is increasing.
-
Passes through coordinate (1, 0)
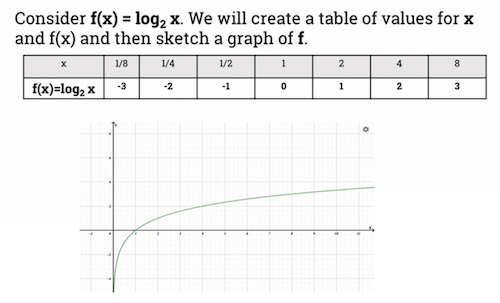
-
Logarithm function with b > 1
-
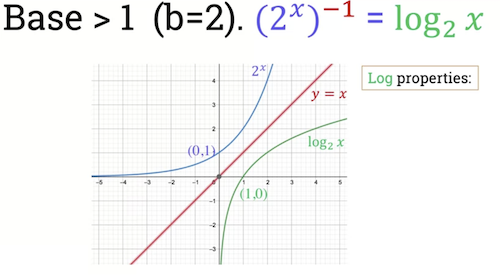
-
Can see the curves are symmetric with respect to red line y = x.
- This is expected as logarthim is inverse of exponential function.
- Can also infer these properties:
- Domain: ($\mathbb{R}^{+}$)
- Range: ($-\infty, \infty$)
- x-intercept:
- increasing on:
-
Example where b < 1
- *$log_{\frac{1}{2}} \ x$
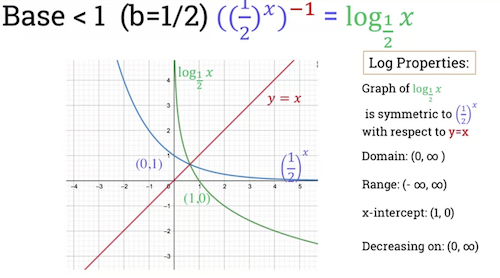
- Can also infer these properties:
- Domain: ($\mathbb{R}^{+}$)
- Range: ($-\infty, \infty$)
- x-intercept:
- decreasing on:
- Natural Logarithm
- Written as
- where
- Graph shows it is an increasing function:
-
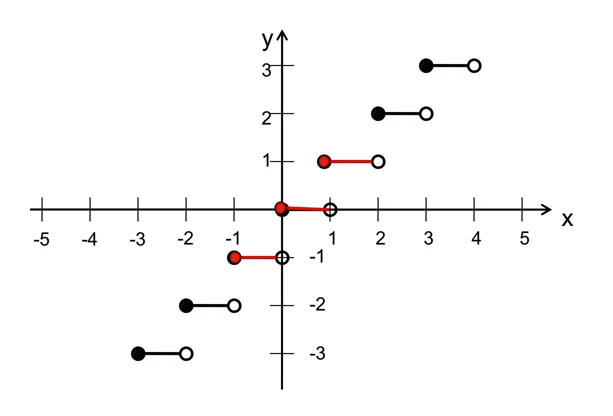
The floor function and ceiling functions
- Floor function
- Takes a real number x as input and returns the largest integer that is less than or equal to
- Function domain and range: .
- Denoted as
- Graph of floor function:
- Examples:
- floor(10) = 10
- floor(1.1) = 1
- floor(1.99) = 1
- floor(-1.1) = -2
- floor(-1.99) = -2
-
- The opposite of the floor function.
- A function
- Takes real number x as input and returns smallest integer greater than or equal to x.
- Denoted as:
-
Graph of ceiling function:
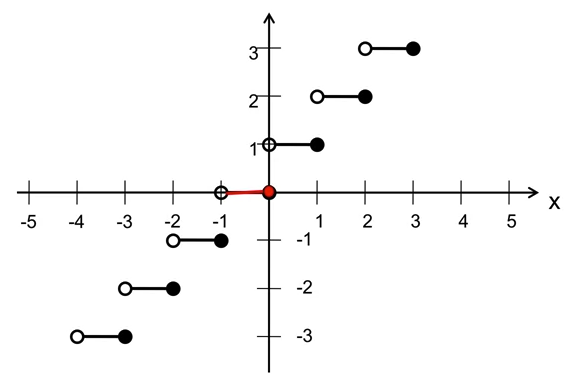
-
Examples:
- ceiling(10) = 10
- ceiling(1.1) = 2
- ceiling(1.99) = 2
- ceiling(-1.1) = -1
- ceiling(-1.99) = -1
- Exercise
- Let be an integer and be a real number. Show that:
- Proof
- Let
- By definition,
- If we add inequality:
- this implies that (by definition)
- Hence, =
2.209 Functions
Real-life examples
-
A function that is not injective (one-to-one) or surjective (onto)
A function that takes a persons name and returns their street number.
Some people live in the same house, hence not injective: but Also, not surjective as the co-domain is but the range will not included many large numbers, depending on the size of the street.
-
A function that is injective but not surjective.
A function that takes a persons username and returns their user id, in the case where the authentication system uses an incrementing integer as the user id and the username is always unique (ala Twitter) and the range of user ids is A username will always map to a unique user id. However, not all user ids in the range will map to usernames, as not all possible registrations has happened yet.
-
A function that is not injective but surjective.
A function that takes all names with < 10 characters and maps to length. All images will most certainly have a preimage, however, lots of names will have the same image.
-
A function that is bijective (invertible)
A similar function to 2, however, the domain is limited to valid registered users
Functions problem sheet
Question 1
- Let and be two sets with and . Which of the following arrow diagrams define functions from to ?
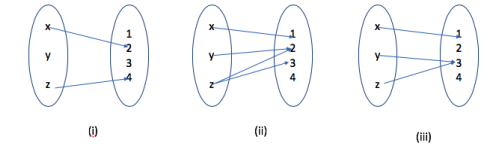
Answer
- (i) is not a function as not every element in has an image in .
- (ii) is not a function as some elements in A map to multiple elements in B.
- (iii) is a function, as all elements of is mapped to unique elements in .
Question 2
Let and be two sets with and .
Let from to defined by the following arrow diagram:
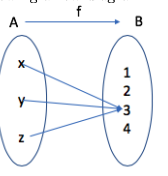
-
Write the domain, the co-domain and the range of .
-
Find and
-
Pre-images for 3: . Pre-images for 1:
Question 3
The Hamming Distance Function is important in coding theory.
It gives the measure of distance between 2 strings of 0's and 1's that have the same length.
Let be the set of all strings of 0's and 1's of length .
The Humming function is defined as follows:
= the number of positions in which s and t have different values.
For n = 5, find
Question 4
Digital messages consist of a finite sequence of 0's and 1's.
When they are communicated across a transmission channel, they are coded to reduce the chance that they will be garbled by integering noise in the transmission lines.
Let A be the set of strings of 0s and 1s and let E and D be the encoding and the decoding function on set A defined for each string. s in A as follows:
E(s) = The string obtained from s by replacing each bit of s with the same bit written three times
D(s) = The string obtained from s by replacing each consecutive triple of three identical bits of s by a single copy of that bit.
Find , , and
- *$E(0110) = 000 111 111 000$
- *$E(0101) = 000 111 000 111$
- *$D(000111000111000111111) = 0101011$
- *$D(111111000111000111000000) = 1 1 0 1 0 1 0 0$
Question 5
Let be three sets.
Let and be two functions defined as follows:
is defined by the following table:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| a | b | a | c | d | d |
g : B → C is defined by the following table.
| a | b | c | d | |
|---|---|---|---|---|
| w | x | y | z |
-
Draw arrow diagrams to represent the function f and g.
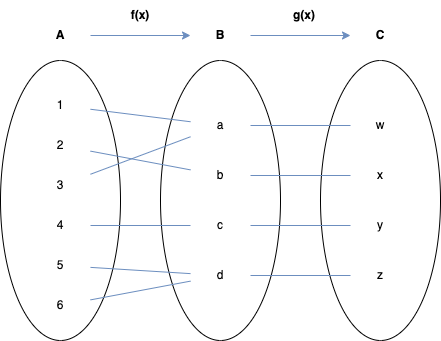
-
List the domain; the co-domain and the range of f and g.
-
f(x)
- $
- set of all actual outputs, which is also co-domain.
-
-
Find f(1), the ancestor (pre-image) of d. and (g o f)(3)
-
-
-
Show that f is not a one to one function.
-
is not injective as .
-
Show that f is an onto function.
-
is surjective as all have at least one pre-image.
-
Show that g is both one to one and onto
-
is injective as , if then
- is surjective as all has at a pre-image.
Question 6
Suppose you read that a function is defined by the formula for all
- is a not a one-to-one function. f(1, 1) = f(2, 2).
- Every ratioal number can be writen with a positive denominator, hence, f is an onto function.
Question 7
Given a function defined by where
-
Plot the graph of a the function where
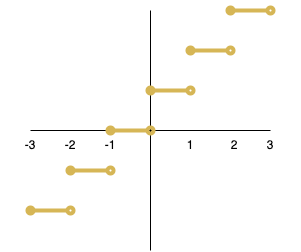
-
Find , ,
-
-
-
Show that is not injective
We can see that , therefore, the function is not injective.
- Show that f is surjective.
For a there exists at least one pre-image in such that .
Therefore every element of the co-domain has a pre-image, and the floor function is an onto function.