Notes by Lex Toumbourou

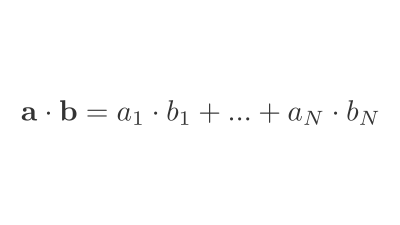
A dot product is an operation between 2 vectors with equal dimensions that returns a number.

The operation is to multiply each element in the first Vector by the corresponding component of the 2nd Vector, then take the sum of the results.

$\mathbf{a} = \begin{bmatrix}a_1 \\ ... \\ a_N\end{bmatrix}, \ \ \mathbf{b} = \begin{bmatrix}b_1 \\ ... \\ b_N\end{bmatrix}$

$\mathbf{a} \cdot \mathbf{b} = a_1 \cdot b_1 + ... + a_N \cdot b_N$

Order doesn't matter: $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$, in other words, it's Commutative.

The dot product is helpful because it tells you about the angle between 2 vectors.

If the vectors are perpendicular to each other, their dot product is 0.

$\begin{bmatrix}1 \\ 0\end{bmatrix} \cdot \begin{bmatrix}0 \\ 1\end{bmatrix} = 1 \cdot 0 + 0 \cdot 1 = 0$

If the vectors are facing in the opposite direction, the dot product is negative.

$\begin{bmatrix}1 \\ 0\end{bmatrix} \cdot \begin{bmatrix}-1 \\ 0\end{bmatrix} = -1 \cdot 1 + 0 \cdot 0 = -1$

We can find the angle in Radians between any 2 vectors if we first know the formula for the dot product:

$\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta$

That's the "length of $\mathbf{a}$" times the "length of $\mathbf{b}$" times "the Cosine ($\cos$) of the angle ($\theta$) between them".

The cosine of an angle is a continuous number between -1 and 1 where:

• $\cos(180°) = -1$
• $\cos(90°) = 0°$
• $\cos(0) = 1$

$\cos(90°) = 0$ explains why the dot product between perpedicular vectors is 0: $|\mathbf{a}| |\mathbf{b}| 0 = 0$

So, to find the angle, we can rearrange to put $\theta$ on the left-hand side: $\theta = \cos^{-1}(\frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|})$.

If we know $\mathbf{a}$ and $\mathbf{b}$ are unit vectors, their lengths will equal 1. So the expression is simply: $\theta = \cos^{-1}(\mathbf{a} \cdot \mathbf{b})$.

We can normalise any vector to convert it into a unit vector by dividing each component by its length: $\mathbf{a} = \frac{\mathbf{a}}{|\mathbf{a}|}$.

We use the dot product throughout game development. For example, it can tell us whether a player turns by comparing their directional vector across frames. We can use it to know whether a player is facing an enemy and so on.

We also use the dot product throughout data science.

We use them in Recommendation Engines.

For example, we can find a vector for each user that represents their movie preferences. One column could describe how much they like scary movies, another for how much they like comedy movies, and so on.

Then for each item, we can create a vector that represents its characteristics. For example, we have a vector with each column describing how scary it is, how funny it is, and so on.

Then, we can take the dot product between a user and each item to determine how likely the user is to enjoy it. The further from 1 each item is, the less likely a user is to like it.

In Machine Learning, we can train a model on a dataset of preference information, often a dataset of user ratings, to learn these vectors. In this context, the vectors are referred to as Embeddings.

Simple Python example:

def dot_product(a, b):
    return sum(a*b for a, b in zip(a, b))

A = [1, 2, 3]
B = [4, 5, 6]

dot_product(A, B)

32

Numpy example:

import numpy as np

np.dot(A, B)

32

Backlinks

• Cross Product
• Cross product introduction
• Matrix Multiplication
• Vector