These are notes from The determinant by 3Blue1Brown from the Essence of linear algebra series.

One way to measure a Matrix Transformation is how much it stretches or squishes space.

Or: "the factor by which a given area increases or decreases after a transformation."

For example, after this [[Matrix Transformation]] $\begin{bmatrix}3 && 0 \\ 0 && 2\end{bmatrix}$, $\hat{i}$ is scaled by a factor of 3, and $\hat{j}$ is scaled by a factor of 2. The rectangular area goes from an area of 1 ( $1 \ \times \ 1$ ) to 6 ( $3 \ \times \ 2$ ), we say the linear transformation has scaled area by 6.

On the other hand, a shear slants the area into a parallelogram, but the base and height remain $1 \ x \ 1$. So the area is unchanged.

Once you know how the area of a single unit square changes, you understand how any given area changes since we know that linear transformations keep gridlines parallel and evenly spaced.

We can use lots of tiny shares to approximate almost any shape.

The amount that we stretch or squish space is called the Determine ([[Matrix Determinate]]).

$\det(\begin{bmatrix}3 && 2 \\ 0 && 2\end{bmatrix}) = 6$

A determine that squishes down space by a factor of 1/2 would be 0.5:

$\det(\begin{bmatrix}0.5 && 0.5 \\ -0.5 && 0.5\end{bmatrix}) = 0.5$

A determinate can also have a negative value. For example:

$\det(\begin{bmatrix}1 && 2 \\ 3 && 4\end{bmatrix}) = -2$

What that means is that the transformation causes the orientation to flip.

In 3d, a determinate tells us how much a volume gets scaled. The name for a parallelogram in 3d space is a parallelepiped.

$\det(\begin{bmatrix}1.0 && 0.0 && 0.5 \\ 0.5 && 1.0 && 0.0 \\ 1.0 && 0.0 && 1.0\end{bmatrix})$

If we have a determinate of 0, the transformation scales space onto a single line or plane in 3d space. That means that the columns of the matrix are linear dependent.

A way to determine if the determinate in 3d space is negative is to use the "right-hand rule."

Point your fingers and thumbs on your right hand like this:

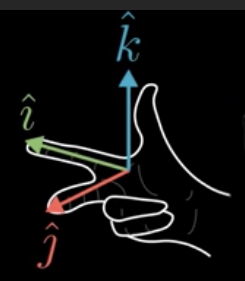
Then if after the transformation, you can only do that with your left hand, you know the determinate is negative.

To calculate determinant in 2d space, we use formula:

$\det(\begin{bmatrix}a && b \\ c && d\end{bmatrix}) = ad - bc$

The intuition for it:

• if c and b are 0, the calculation would be $ad - 0$. That means the determinate is just how much you scale in the x-direction and how much y.

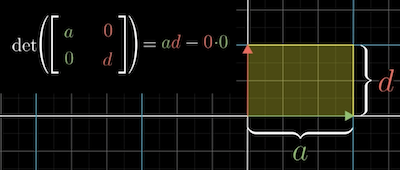
• Even if either b or c = 0, the area would turn into a parallelogram and remain the same area.

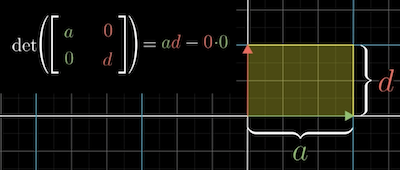
Computing the determinants by hand can be done, and you get better with practice.

There is even a formula for the 3d determinants.

However, computing the determinate doesn't fall within the "essence" of linear algebra, but understanding it visually does.

Last note: If you take the product of 2 matrices, it's the same as the products of both of the two matrices:

$\det(M_1 \ M_2) =\det(M_1) \det(M_2)$

Maths/LinearAlgebra/Determinant