Notes from Three-dimensional linear transformations by 3Blue1Brown from the Essence of linear algebra series

The core ideas in 2d linear algebra carry over into higher dimensions.

We can represent a linear transformation with 3d vectors as inputs and 3d vectors as outputs as a 3d grid.

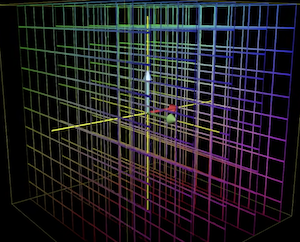
Like 2d space, linear transformations in 3d keep the grid lines evenly spaced and parallel, and the origin remains fixed.

In 3d space, we have basis vectors that describe the space. However, in 3d space we have 3 standard basis vectors: $\hat{i} = \begin{bmatrix}1 \\ 0 \\ 0\end{bmatrix}$, $\hat{j} = \begin{bmatrix}0 \\ 1 \\ 0\end{bmatrix}$ and $\hat{k} = \begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix}$

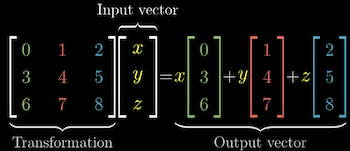
We can record where the basis vectors land after a transformation as columns of a 3x3 matrix. That represents a Matrix Transformation To find where a 3d vector lands after a transformation, we can use identical reasoning to 2d dimensional space.

We can think of each component of a vector as instructions for how to scale each basis vector.

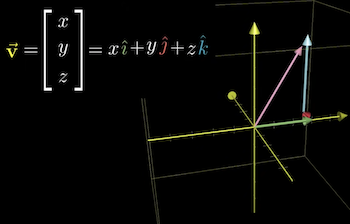
To find where a vector lands after a transformation, we multiple the coordinates by the corresponding columns of the matrix.

3d Matrix Multiplication is fundamental for computer graphics and robotics.

Maths/LinearAlgebra/Matrix