Week 15 - Trees A
8.101 Introduction
- Trees are usually represented upside down in Computer Science:
- Trees have many use cases:
- Organisation charts.
- Computer file systems.
- Used to find shortest path in graph.
- Used to construct efficient algorithms to locate items in a list.
- Used in games such as checkers and chess to determine winning strategies.
- Use to model procedures carried out as a sequence of decisions.
- Binary tree is fundamental data structure in high-level programming.
8.103 Definition of a tree
-
- A graph G is called an acyclic graph if and only if G has no cycles.
- No loops and no parallel edges.
- contains a cycle B, C, D, E
- contains no cycle

- A graph G is called an acyclic graph if and only if G has no cycles.
-
Definition of a tree
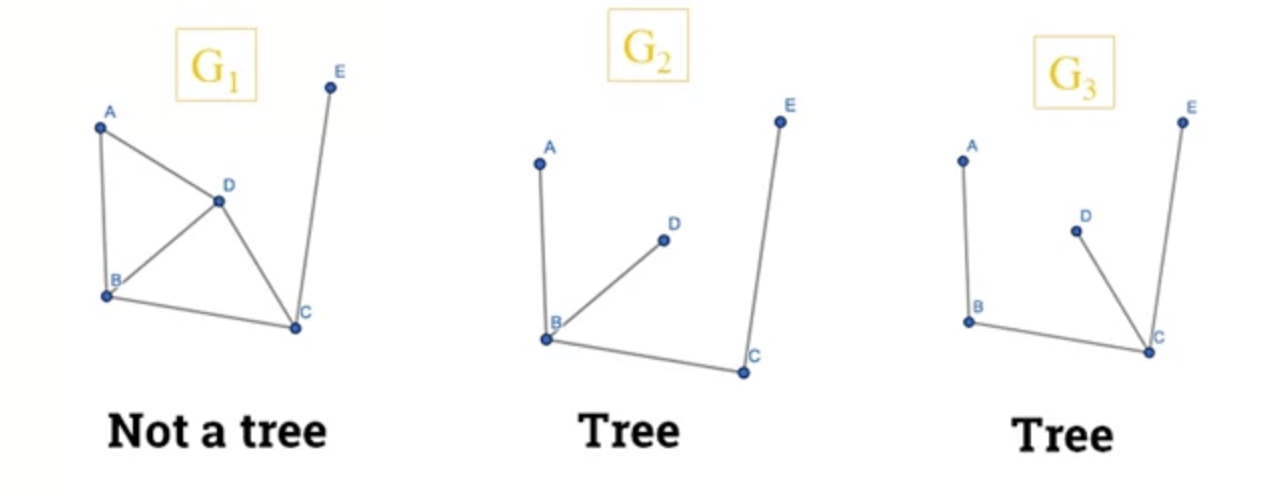
- A tree is a connected acyclic undirected graph.
- Hence, a tree can have neither loops nor edges.
-
A disconnected graph containing no cycles is called a Forest.
-
Theorem 1
- An undirected graph is a tree if and only if there is a unique simple path between any 2 of its vertices.
- We can prove by contradiction
- In this example, we show that if there exists a 2nd path P2 between B and I, we can see that this results in a cycle. Hence, it is not a tree.
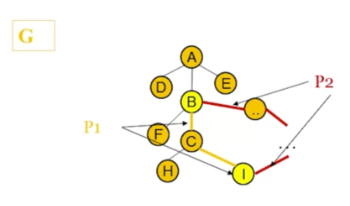
-
Theorem 2
- A tree with n vertices has n-1 edges.
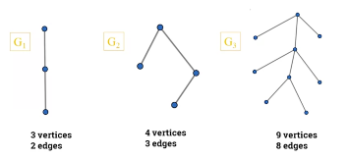
- A tree with n vertices has n-1 edges.
-
Rooted trees
- A rooted tree is when one vertex has been designated as the root, and every edge is directed away from the root.
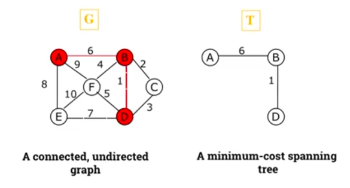
8.105 Spanning trees of a graph
-
- In many real-life problems like Internet multicasting, we need to identify trees that exist within a graph.
- A spanning tree of graph G is a connected sub graph of G which contains all vertices of G, but with no cycles.
-
Example
- is a connected graph, , , and are spanning trees.
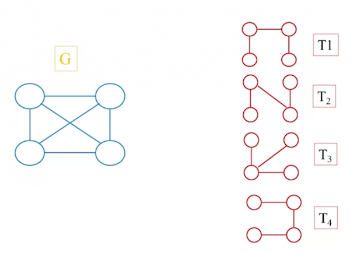
- is a connected graph, , , and are spanning trees.
-
To get a spanning tree of graph G.
-
- Keep all verticies of G.
-
- Break all cycles but keep the tree connected.
-
- Examples of spanning trees

-
Two spanning trees are said to be isomorphic if there is a bijection preserving adjaceny between the two trees.
- Some spanning trees of a graph might be isomorphic to each other: ie they're the same.
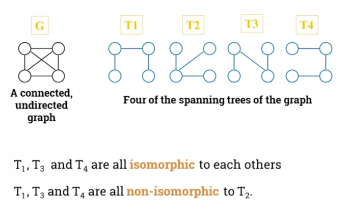
- In this example, we would only draw and , or and or and if we were asked for non-isomorphic trees.
8.107 Min Spanning Tree
- Example of a use case:
- Suppose you want to supply houses with:
- electric power
- water pipes
- sewage lines
- telephone lines
- To keep costs down, you could connect with spanning tree (power lines, for example)
- However, houses are not equal distance apart.
- To reduce costs even further, connect the houses with a minimum-cost spanning tree.
- Suppose you want to supply houses with:
- Spanning trees costs
- Suppose you have a connected undirected graph with a weight (or cost) associated with each edge.
- The cost of a spanning tree would be the sum of the costs of its edges.
-
Weight of a spanning tree
- In this image, there are 3 spanning trees of graph each with separate costs
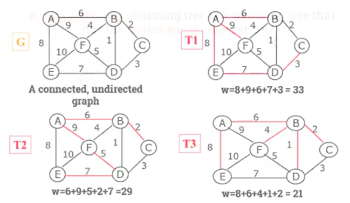
- In this image, there are 3 spanning trees of graph each with separate costs
-
Minimum spanning trees
- Minimum-cost spanning tree is a spanning tree that has the lowest weight (lowest cost).
-
Finding spanning trees
- There are 2 algorithms for finding minimum-cost spanning trees, and both are greedy algorithms:
- Kruskal's Algorithm
- Prim's Algorithm
- There are 2 algorithms for finding minimum-cost spanning trees, and both are greedy algorithms:
-
- Start with cheapest edge in spanning tree.
- Repeatedly: keep adding cheapest edge that does not create a cycle.
-
Step 1.
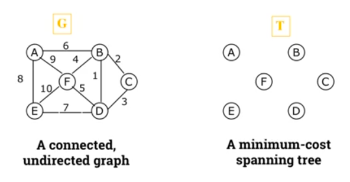
-
Step 2.
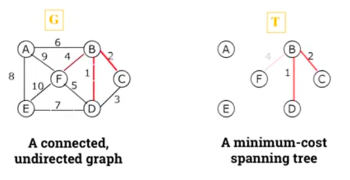
-
And so on...
- Prim's Algorithm
- Start with any node in spanning tree.
- Repeatedly add the cheapest edge, and the node it leads to, for which the node is not already in that spanning tree.