Week 2 - Sets B

My notes from Week 2 from Discrete Mathematics Course Notes.

Lesson 1.2 Set representation and manipulation

1.201 The representation of a set using Venn diagrams

• Universal Set
  • A set containing everything.
  • Represented by letter $U$.
• Complement
  • Represented as: $\bar{A}$
  • All the elements in the universal set $U$ but not in $A$: $\bar{A} = U - A$
  • The union of a set and its compliment, is equal to universal set: $\bar{A} \cup A = U$

• Venn Diagram

  • Used to visualise the possible relations among a collection of sets.

  • In this example, the red area represents the union of A and B:

    

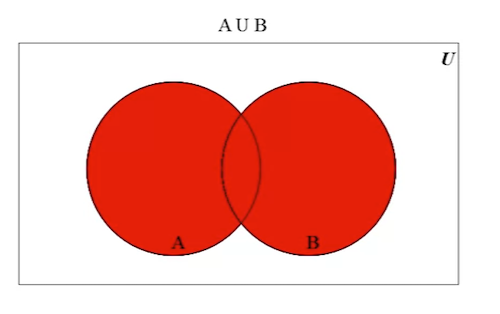
  • In this example, the red area represents the intersection of A and B:

    

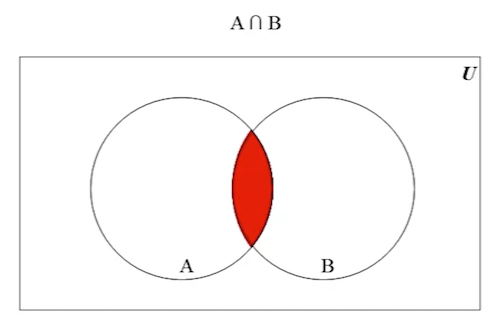
  • In this example, the set difference:

    

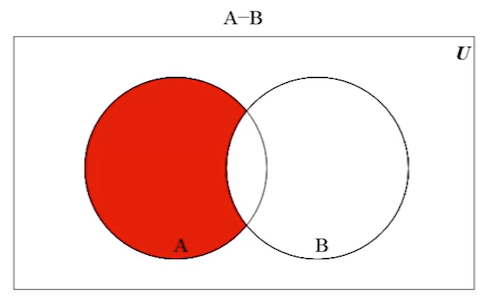
  • In this example, it shows the symmetric difference between A and B

    

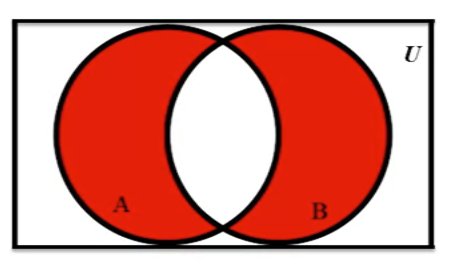
  • Can use a Venn Diagram to show that each sets are equivalent.

    

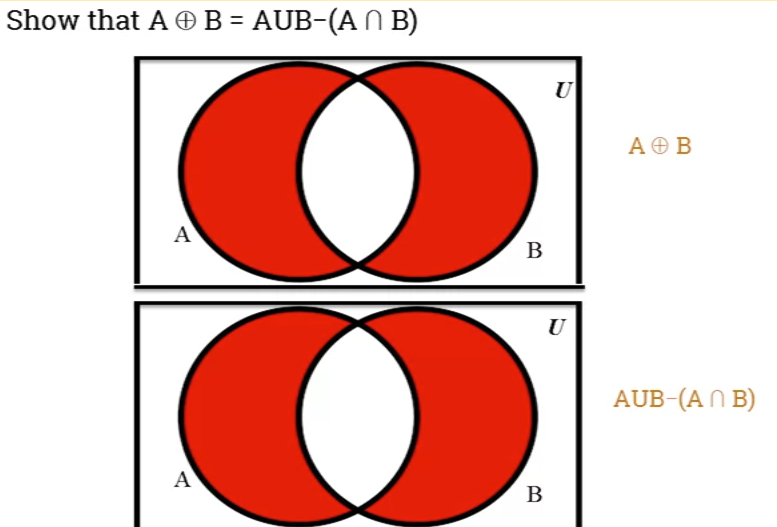
1.203 De Morgan's laws

• De Morgan's Laws
  • By Augustus De Morgan (1806 - 1871), a British mathematician.
  • Describe how statements and concepts are related through opposites.
  • Example from set theory:
    • De Morgan's laws relate to the Intersection and Union of sets through their complements.
  • The structure of De Morgan's laws, whether applied to sets, propositions or logic gates is always the same.
  • Law #1: Compliment of the union of 2 sets, $A$ and $B$ is equal to intersection of complements:
    • $\overline{A \cup B} = \bar{A} \cap \bar{B}$
      • $A = \{a, b\}, B = \{b ,c, d\}$
      • $\overline{A \cup B}$ = $\overline{\{a, b, c, d}\}$ = $\{\}$
      • $\overline{A} = \{c, d\}$, $\overline{B} = \{a\}$,
        • $\overline{A} \cap \overline{B} = \{\}$,
  • Law #2: Complement of the intersection of 2 sets A and B, is equal to union of their complements.
    • $\overline{A \cap B} = \bar{A} \cup \bar{B}$
      • $A = \{a, b\}, B = \{b, c, d\}$
      • $\overline{A \cap B} = \{a, c, d\}$
      • $\bar{A} \cup \bar{B} = \{a, c, d\}$

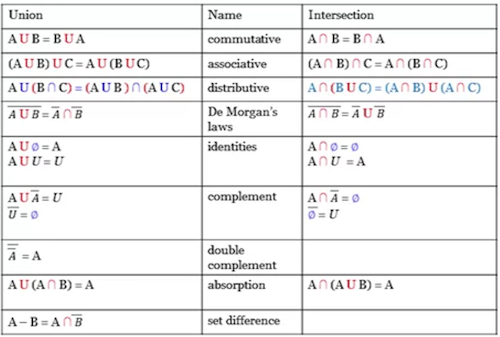
1.205 Laws of sets: Commutative, associative and distributives

• Commutative Operation
  • An operation where order does not affect the results.
    • Additional is commutative: $2 + 3 = 3 + 2$
    • Multiplication is commutative: $2 x 3 = 3 x 2$
    • Subtraction is not commutative: $2 - 3 \neq 3 - 2$
  • Set union is commutative:
    • $A \cup B = B \cup A$
  • Set intersection is commutative:
    • $A \cap B = B \cap A$
  • Symmetric difference is commutative:
    • $A \oplus B = B \oplus A$
  • Set difference is not commutative:
    • $A - B \neq B - A$
• Associativity Operation
  • Concerns grouping of elements in an operation.
    • An example from algebra, the additional of numbers is associative:
      • $(a + b) + c = a + (b + c)$
  • The grouping of elements does not affect the results for union, set intersection or symmetric difference.
  • Set union is associative:
    • $(A \cup B) \cup C = A \cup (B \cup C)$
  • Set intersection is associative:
    • $(A \cap B) \cap C = A \cap (B \cap C)$
  • Symmetric difference is associative:
    • $(A \oplus B) \oplus C = A \oplus (B \oplus C)$
  • Set difference is not associate:
    • $(A - B) - C \ne A - (B - C)$
• Distributivity
  • Sometimes called the distributive law of multiplication and division.
    • Example in algebra: Given 3 numbers a, b, c: $a(b + c) = ab + ac$
  • Set union is distributive over set intersection:
    • $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
  • Set intersection is distributive over set union
    • $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$

• Set Identities

  

  • Set identities can be used to simplify set expressions.
    • Example:
      • Show that $\overline{(A \cap B) \cup \overline{B}} = B \cap \overline{A}$
      • $= \overline{(A \cap B) \cup \overline{B}} = \overline{(A \cap B)} \cap \overline{\overline{B}}$ -- De Morgan's law.
      • $=\overline{(A \cap B)} \cap B$ -- double complement
      • $=(\overline{A} \cup \overline{B}) \cap B$ -- De Morgan's law.
      • $=B \cap (\overline{A} \cup \overline{B})$ -- commutative.
      • $=(B \cap \overline{A}) \cup (B \cap \overline{B})$ -- distributive.
      • $= (B \cap \overline{A}) \cup \emptyset$ -- identity
      • $= B \cap \overline{A}$ -- complement

1.207 Partition of a set

• Partition
  • To partition an object is to separate it into parts so each parts are separate from each other, but together make up the whole object.
  • A partition of a set $A$ is a set of subsets of $A$ such that:
    • all the subsets of A are disjointed.
    • the union of all subsets $A_i$ is equal to $A$.

  • Example:

    

    • $A_1 \cap A_2 = A_2 \cap A_3 = .... A_4 \cap A_5 = \emptyset$
    • $A = A_1 \cup A_2 \cup A_3 \cup A_4 \cup A_5$
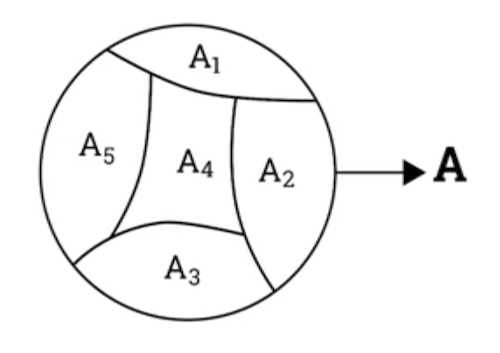
    • $\{A_1, A_2, A_3, A_4, A_5\}$ is a partition on $A$
    • Disjoint Sets
      • Two sets are considered disjointed if and only if their intersection is an empty set.
    • $A \cap B = \emptyset$

Peer-graded Assignment: 1.209 Sets

Part 1

Question

Given three sets A, B and C, prove that: $|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - | A \cap C| - |B \cap C|+ |A\cap B\cap C|$

Proof

$$ \begin{align} |A \cup B \cup C| &= |A \cup (B \cup C)| \ & = |A| + |B \cup C| - | A \cap (B \cup C)| \text{ --- IEP} \ & = |A| + |B \cup C| - |(A \cap B) \cup (A \cap C)| \text{ \ \ \ --- distributive law} \ & = |A| + (|B| + |C| - |B \cap C|) - (|A \cap B| + |A \cap C| - |(A \cap B) \cap (A \cap C)|) \ & = |A| + |B| + |C| - |B \cap C| - |A \cap B| - |A \cap C| + |(A \cap B) \cap (A \cap C)| \ & = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C| \ \

\text{ since } |(A \cap B) \cap (A \cap C)| &= |A \cap B \cap C| \end{align} $$

Part 2

Question

Let A and B two subsets of the universal set $U = \{ x: x \in \mathbb{Z} \text{ and } 0 \leq x<20\}$. $A$ is the set of even numbers in $U$, where $B$ is the set of odd numbers in $U$.

Use the listing method to list the elements of the following sets: $A \cap \overline{B}$, $\overline{A\cap B}$ , $\overline{A\cup B}$ and $\overline{A\oplus B}$

Answer

$A \cap \overline{B}$ = $\{0, 2, 4, 6, 8, 10, 12, 14, 16, 18\}$

$\overline{A \cap B}$ = $\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19\}$

$\overline{A \cup B}$ = $\{\}$

$\overline{A \oplus B}$ = $\{\}$