Week 2 - Sets B
My notes from Week 2 from Discrete Mathematics Course Notes.
Lesson 1.2 Set representation and manipulation
1.201 The representation of a set using Venn diagrams
- Universal Set
- A set containing everything.
- Represented by letter .
- Complement
- Represented as:
- All the elements in the universal set but not in :
- The union of a set and its compliment, is equal to universal set:
-
- Used to visualise the possible relations among a collection of sets.
-
In this example, the red area represents the union of A and B:
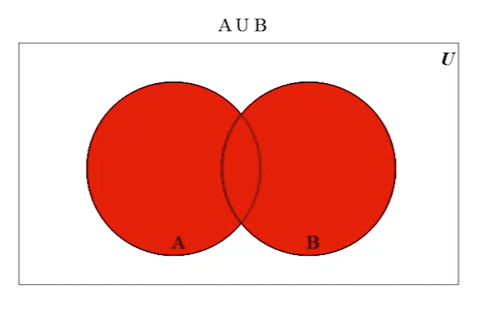
-
In this example, the red area represents the intersection of A and B:
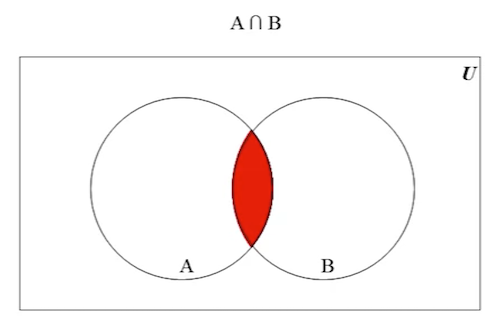
-
In this example, the set difference:
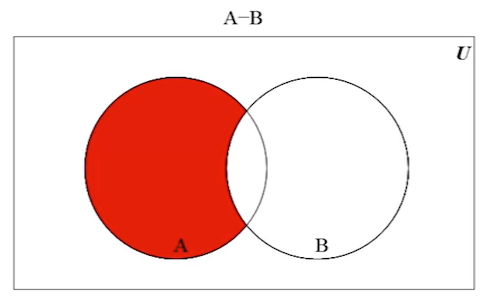
-
In this example, it shows the symmetric difference between A and B
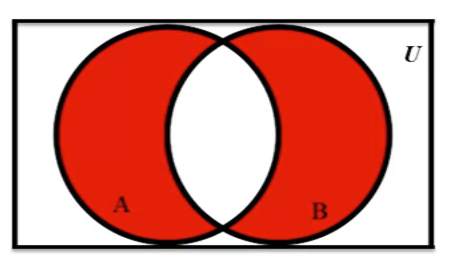
-
Can use a Venn Diagram to show that each sets are equivalent.
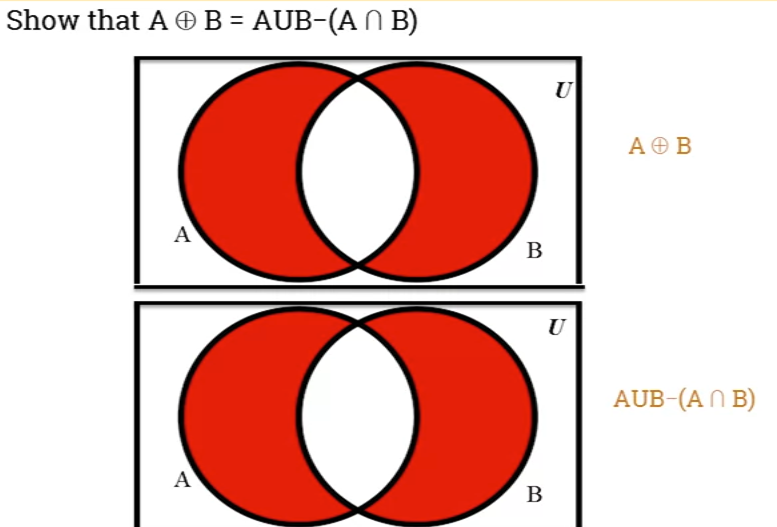
1.203 De Morgan's laws
- De Morgan's Laws
- By Augustus De Morgan (1806 - 1871), a British mathematician.
- Describe how statements and concepts are related through opposites.
- Example from set theory:
- De Morgan's laws relate to the Intersection and Union of sets through their complements.
- The structure of De Morgan's laws, whether applied to sets, propositions or logic gates is always the same.
- Law #1: Compliment of the union of 2 sets, and is equal to intersection of complements:
- = =
- , ,
- ,
- Law #2: Complement of the intersection of 2 sets A and B, is equal to union of their complements.
1.205 Laws of sets: Commutative, associative and distributives
- Commutative Operation
- An operation where order does not affect the results.
- Additional is commutative:
- Multiplication is commutative:
- Subtraction is not commutative:
- Set union is commutative:
- Set intersection is commutative:
- Symmetric difference is commutative:
- Set difference is not commutative:
- An operation where order does not affect the results.
- Associativity Operation
- Concerns grouping of elements in an operation.
- An example from algebra, the additional of numbers is associative:
- An example from algebra, the additional of numbers is associative:
- The grouping of elements does not affect the results for union, set intersection or symmetric difference.
- Set union is associative:
- Set intersection is associative:
- Symmetric difference is associative:
- Set difference is not associate:
- Concerns grouping of elements in an operation.
- Distributivity
- Sometimes called the distributive law of multiplication and division.
- Example in algebra: Given 3 numbers a, b, c:
- Set union is distributive over set intersection:
- Set intersection is distributive over set union
- Sometimes called the distributive law of multiplication and division.
-
- Set identities can be used to simplify set expressions.
- Example:
- Show that
- -- De Morgan's law.
- -- double complement
- -- De Morgan's law.
- -- commutative.
- -- distributive.
- -- identity
- -- complement
- Example:
- Set identities can be used to simplify set expressions.
1.207 Partition of a set
- Partition
- To partition an object is to separate it into parts so each parts are separate from each other, but together make up the whole object.
- A partition of a set is a set of subsets of such that:
- all the subsets of A are disjointed.
- the union of all subsets is equal to .
-
Example:
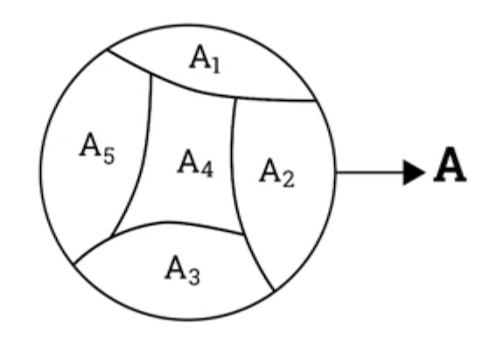
- is a partition on
- Disjoint Sets
- Two sets are considered disjointed if and only if their intersection is an empty set.
Peer-graded Assignment: 1.209 Sets
Part 1
Question
Given three sets A, B and C, prove that:
Proof
$$ \begin{align} |A \cup B \cup C| &= |A \cup (B \cup C)| \ & = |A| + |B \cup C| - | A \cap (B \cup C)| \text{ --- IEP} \ & = |A| + |B \cup C| - |(A \cap B) \cup (A \cap C)| \text{ \ \ \ --- distributive law} \ & = |A| + (|B| + |C| - |B \cap C|) - (|A \cap B| + |A \cap C| - |(A \cap B) \cap (A \cap C)|) \ & = |A| + |B| + |C| - |B \cap C| - |A \cap B| - |A \cap C| + |(A \cap B) \cap (A \cap C)| \ & = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C| \ \
\text{ since } |(A \cap B) \cap (A \cap C)| &= |A \cap B \cap C| \end{align} $$
Part 2
Question
Let A and B two subsets of the universal set . is the set of even numbers in , where is the set of odd numbers in .
Use the listing method to list the elements of the following sets: , , and
Answer
=
=
=
=