Notes by Lex Toumbourou

Introduction to matrices

Matrices, vectors, and solving simultaneous equation problems

• Matrices are objects that "rotate and stretch" vectors.

• Given this simultaneous equation:

  $2a + 3b = 8$

  $10a + 1b = 13$

  • We can express as a matrix product:

    $\begin{bmatrix}2 & 3 \\ 10 & 1 \end{bmatrix}\begin{bmatrix}a \\ b\end{bmatrix} = \begin{bmatrix}8 \\ 13\end{bmatrix}$

• A matrix product multiplies each row in A by each column in B (see Matrix Multiplication

• So we could rephrase the question as which vector transforms to give you the answer?

• What happens when you multiply the matrix by the Basis Vectors:

  $\begin{bmatrix}2 & 3 \\ 10 & 1 \end{bmatrix} \begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}2 \\ 10\end{bmatrix}$

  $\begin{bmatrix}2 & 3 \\ 10 & 1 \end{bmatrix} \begin{bmatrix}0 \\ 1\end{bmatrix} = \begin{bmatrix}3 \\ 1\end{bmatrix}$

  It takes the basis vector and moves it to another place:

  

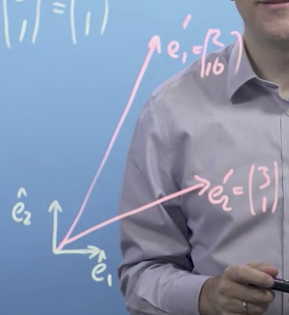
  So the matrix "moves" the basis vectors.

  We can think of a matrix as a function that operates on input vectors and gives us new output vectors.

• Why is it called "Linear algebra"?

  • Linear because it takes input values and multiplies them by constants.
  • Algebra because it's a notation for describing mathematical objects
  • "So linear algebra is a mathematical system for manipulating vectors in the spaces described by vectors."
  • The "heart of linear algebra": the connection between simultaneous equations and how matrices transform vectors.

Matrices in linear algebra: operating on vectors

How matrices transform space

• We know that we can make any vector out of a sum of scaled versions of $\hat{e}_1$ and $\hat{e}_2$
• A consequence of the scalar addition and multiplication rules for vectors, we know that the grid lines of our space don't change.
• If we have matrix $A=\begin{bmatrix}2 & 3 \\ 10 & 1\end{bmatrix}$ and a matrix $r= \begin{bmatrix}a \\ b\end{bmatrix}$ and a result $r' = \begin{bmatrix}8 \\ 13\end{bmatrix}$ with relationship: $A r = r'$
• If we multiply $r$ by a number $n$, then apply to $Ar$, we get the result by n: $A (nr) = nr'$
• If we multiple $A$ by the vector $r+s$, we get $Ar+As$: $A(r+s)=Ar+As$

• If we think of $r$ and $s$ as the original basis vectors:

  $A (n\hat{e}_i +m\hat{e}_2) = A n\hat{e}_1 + A m\hat{e}_2$

• An example:

  • Given this expression: $\begin{bmatrix}2 & 3 \\ 10 & 1\end{bmatrix} \begin{bmatrix}3 \\ 2\end{bmatrix} = \begin{bmatrix}12 \\ 32\end{bmatrix}$
  • We can rewrite as: $\begin{bmatrix}2 & 3 \\ 10 & 1\end{bmatrix} \left(3 \begin{bmatrix}1 \\ 0\end{bmatrix} + 2 \begin{bmatrix}0 \\ 1\end{bmatrix} \right) = \begin{bmatrix}12 \\ 32\end{bmatrix}$
  • Which is the same as: $3 \left( \begin{bmatrix}2 & 3 \\ 10 & 1\end{bmatrix} \begin{bmatrix}1 \\ 0\end{bmatrix} \right) + 2 \left( \begin{bmatrix}2 & 3 \\ 10 & 1\end{bmatrix} \begin{bmatrix}0 \\ 1\end{bmatrix} \right)$
  • Simplified to: $3 \begin{bmatrix}2 \\ 10\end{bmatrix} + 2 \begin{bmatrix}3 \\ 1\end{bmatrix}$
  • Which we can simplify to: $\begin{bmatrix}12 \\ 32\end{bmatrix}$
• "We can think of a matrix multiplication as just being the multiplication of the vector sum of the transformed basis vectors."

Types of matrix transformation

• Identity Matrix (00:00-00:53)

  • A matrix that doesn't change any vector/matrix it multiplies. Like 1 in scalar math.

    $\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix}a \\ b\end{bmatrix} = \begin{bmatrix}a \\ b\end{bmatrix}$

• A scaling matrix: a scaled-up identity matrix that can scale a vector.

  $\begin{bmatrix}3 & 0 \\ 0 & 2\end{bmatrix}$

  

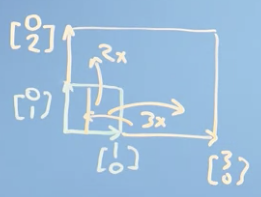
• If you have a negative number for one of the axes, you could flip a vector.

  $\begin{bmatrix}-1 & 0 \\ 0 & 2\end{bmatrix}$

  

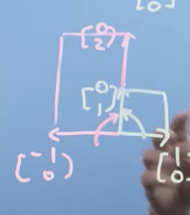
• If you have negative numbers in each of the diagonal positions, you invert the vector.

  $\begin{bmatrix}-1 & 0 \\ 0 & -1\end{bmatrix}$

• You can switch the axes in a vector with this matrix:

  $\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$

• You can perform a vertical mirror of a vector with the matrix

  $\begin{bmatrix}0 & -1 \\ -1 & 0\end{bmatrix}$

• You can shear a vector with this matrix

  $\begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix}$

  

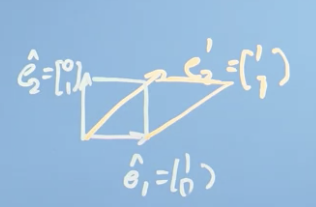
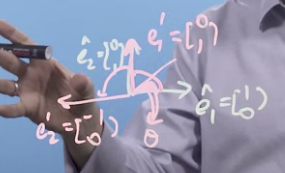
• You can rotate a vector with this matrix

  $\begin{bmatrix}0 & -1 \\ 1 & 0 \end{bmatrix}$

• In general, the matrix for a rotation in 2d is: $\begin{bmatrix}\cos\theta & \sin\theta \\ -\sin\theta & \cos\theta\end{bmatrix}$ where $\theta$ describes the angle between vectors:

  

• We store a digital image as a collection of colored pixels at their particular coordinates on a grid. If we apply a matrix transformation to the coordinates of each pixel in an image, we transform the picture as a whole.

Composition or combination of matrix transforms

• You can make a shape change for a vector out of any combination of rotations, shears, structures, and inverses.

• I can apply $A_1$ to $r$ then $A_2$ to that result:

  $A_2(A_1 r)$

  • Alternatively, you can first apply $A_2$ to $A_i$ to get the same result.
  • Note that $A_1$ applied to $A_2$ isn't the same as $A_2$ to $A_1$: the order matters.
  • Therefore, Matrix multiplication isn't commutative.
  • Matrix multiplication is associative: $A_3 \cdot (A_2 \cdot A_1) = (A_3 \cdot A_2) \cdot A_1$

Matrix inverses

Solving the apples and bananas problem: Gaussian Elimination

• Revisit the Apples and Bananas problem

  $\begin{bmatrix}2 & 3 \\ 10 & 1\end{bmatrix}\begin{bmatrix}a \\ b\end{bmatrix} = \begin{bmatrix}8 \\ 13 \end{bmatrix}$

  That's a matrix multiplied by a vector.

  We can call the matrix $A$, vector $r$ and output $s$: $A r = s$

• Inverse Matrix (00:59-02:04)

  • Can we find another matrix that, when multiplied by A, gives us the identity matrix? $A^{-1} A = I$
    • We consider the "inverse" of $A$ since it reverses A and gives you the identity matrix.
  • We can then add the inverse to both sides of the expression: $A^{-1} A r = A^{-1}s$.
  • Since we know that $A^{-1} A$ is simply the identity matrix, we can simplify: $r = A^{-1} s$
  • So, if we can find the inverse of $A^{-1}$, we can solve the apples and bananas problem.

• Solving matrix problems with Elimination and Back Substitution (02:15-08:00)

  • We can also solve the apples / bananas problem with just substitution.

    $\begin{bmatrix}1 & 1 & 3\\ 1 & 2 & 4 \\ 1 & 1 & 2\end{bmatrix}\begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}15 \\ 21 \\ 13 \end{bmatrix}$

    We can take row 1 off row 2 and 3.

    $\begin{bmatrix}1 & 1 & 3\\ 0 & 1 & 1 \\ 0 & 0 & -1\end{bmatrix}\begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}15 \\ 6 \\ -2 \end{bmatrix}$

    We can multiply row c by -1, which gives us the value of c: $c = 2$.

    $\begin{bmatrix}1 & 1 & 3\\ 0 & 1 & 1 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}15 \\ 6 \\ 2 \end{bmatrix}$

    We know we have what's called a Triangular Matrix, which is a matrix where everything below the "body diagonal" is 0. We have reduced the matrix to Row Echelon Form.

    We can take c from each of the rows.

    Take c from the first row and 2nd row.

    $\begin{bmatrix}1 & 1 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}9 \\ 4 \\ 2 \end{bmatrix}$

    Now we know that $b = 4$. We can remove b from the first row.

    $\begin{bmatrix}1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}5 \\ 4 \\ 2 \end{bmatrix}$

  • So we've first done Elimination to get to triangular form.

  • Then do Back Substitution to get a solution to the problem.
  • This is one of the most computationally efficient ways to solve the problem.
  • However, we have solved the problem, but we haven't solved it in a general way.

Going from Gaussian Elimination to finding the inverse matrix

• Using Elimination to find the Inverse Matrix (00:00-07:26)

  • Here, we have a 3x3 matrix $A$ multiplied by its inverse $B$, which equals the identity matrix.

    $A \cdot B = I$

    $\begin{bmatrix}1 & 1 & 3 \\ 1 & 2 & 4 \\ 1 & 1 & 2\end{bmatrix} \begin{bmatrix}b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33}\end{bmatrix} = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$

  • We can start by just solving the first column of the inverse matrix:

    $\begin{bmatrix}1 & 1 & 3 \\ 1 & 2 & 4 \\ 1 & 1 & 2\end{bmatrix} \begin{bmatrix}b_{11} \\ b_{21} \\ b_{31} \end{bmatrix} = \begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix}$

    Or do it all at once.

  • We can take the first row off the 2nd and third row, and the same from the identity matrix

    $\begin{bmatrix}1 & 1 & 3 \\ 0 & 1 & 1 \\ 0 & 0 & -1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ -1 & 1 & 0 \\ -1 & 0 & 1\end{bmatrix}$

    Then multiply the last row by -1 to put the left matrix in triangular form.

    $\begin{bmatrix}1 & 1 & 3 \\ 0 & 1 & 1 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ -1 & 1 & 0 \\ 1 & 0 & -1\end{bmatrix}$

    Can substitute the 3rd row back into the other rows. Take 1x of the 3rd row off the 2nd and 3x of the 3rd row of the 1st.

    $\begin{bmatrix}1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}-2 & 0 & 3 \\ -2 & 1 & 1 \\ 1 & 0 & -1\end{bmatrix}$

    Then take the 2nd row off the first.

    $\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}0 & -1 & 2 \\ -2 & 1 & 1 \\ 1 & 0 & -1\end{bmatrix}$

    So now we have an inverse of A!

• There are more computationally efficient ways to do this. In practice, you'll call the solver function of your computer program. In Numpy, it's: numpy.linalg.inv(A) which just calls numpy.linalg.solve(A,I)

Special matrices and Coding up some matrix operations

Determinates and inverses

• Matrix Determinate (00:00-05:36)
• A matrix like this scales space: $\begin{bmatrix}a & 0 \\ 0 & d\end{bmatrix}$ by a factor of $ad$.

• $ab$ is called the "determinate" of the transformation matrix.

  

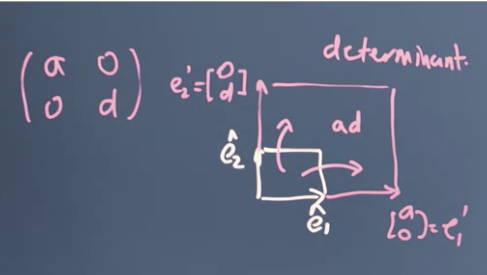
• If you have matrix $\begin{bmatrix}a & b \\ 0 & d\end{bmatrix}$ you create a parallelogram, but the area is still $ad$

  

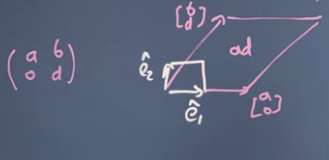
• If you have a general matrix $\begin{bmatrix}a & b \\ c & d\end{bmatrix}$, the area creating by transforming the basis vectors is $ad-bc$

  

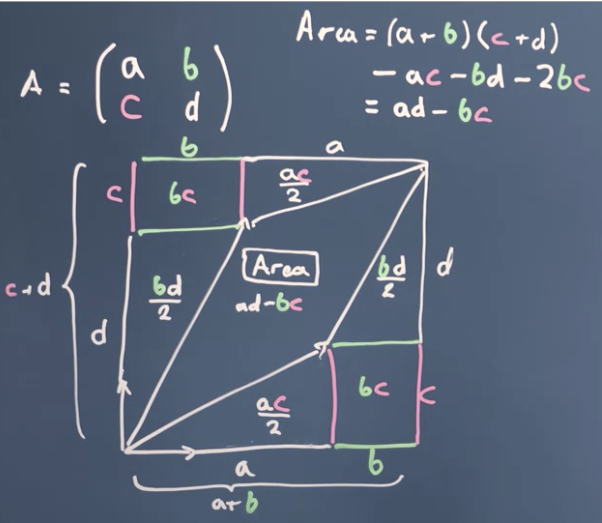
• We denote finding the determinate as $|A|$.

• A standard method for finding the inverse of a matrix is to flip the terms on the leading diagonal and to flip the terms on the other diagonal, then multiplying by 1 / determinate:

  $\begin{bmatrix}a & b\\c & d\end{bmatrix}^{-1} = \frac{1}{ad-bc} \begin{bmatrix}d & -b\\-c & a\end{bmatrix}$

• Knowing how to find the determinate in the general case is generally not a valuable skill. We can ask our computer to do it: $\det(A)$.

• When a matrix doesn't have a Matrix Inverse (05:38-09:19)
• Consider this matrix: $A=\begin{bmatrix}1 & 2\\1 & 2\end{bmatrix}$
  • It transforms $\hat{e}_1$ and $\hat{e}_2$ to be on the same line.
  • The determinate of A is 0: $|A|=0$
  • If you had a 3x3 matrix, where one of the Basis Vectors was just a multiple of the other 2, ie it isn't linearly independent, the new space would be a plane, which also has a determinate of 0.

• Consider another matrix. This one doesn't describe a new 3d space. It collapses into a 2d space.

  $\begin{bmatrix}1 & 1 & 3\\1 & 2 & 4\\2 & 3 & 7\end{bmatrix} \begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}12 \\ 17 \\ 29 \end{bmatrix}$

  • row 3 = row 1 + row 2
  • col 3 = 2 col 1 + col 2

  When you try to solve, you don't have enough information. $0c = 0$ is true, but any number of solutions would work for that.

  $\begin{bmatrix}1 & 1 & 3 \\ 0 & 1 & 1 \\ 0 & 0 & 0\end{bmatrix} \begin{bmatrix}a \\ b \\ c\end{bmatrix} = \begin{bmatrix}12 \\ 5 \\0 \end{bmatrix}$

  So, where the Basis Vectors that describe the matrix aren't linear independent, which means the determinate is 0, you cannot find the inverse matrix.

• Another way to think of inverse matrix is something that undoes a transformation and returns the original matrix.