Linear Transformations and Matrices
Notes from Linear transformations and matrices by 3Blue1Brown from the Essence of linear algebra series
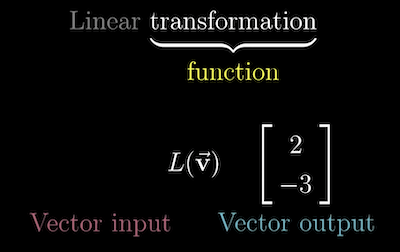
Breaking down "Linear Transformation":
- Transform: another name for a function, in that it takes an input and returns the output.
- However, a "transformation" implies the ability to move the transformation as "movement".
- Linear: limits the types of transformation to ones that have these visual properties:
- All lines, remain lines.
- Origin remains fixed in place.
- This keeps the grid lines parallel and evenly spaced.
To record a transformation numerically, you only need to store where the Basis Vectors, and land.
Consider vector
We know it's just a linear combination of and :
We know grid lines become evenly spaced.
So, after applying the transformation, the property: still applies, it's just the basis vectors that have been transformed.
That means we can fully describe a 2d transformation with four numbers (2 vectors).
We put these numbers into a 2x2 matrix, called a Matrix Transformation. Each column is one of the transformed Basis VectorsTransformation matrix
So for any vector, we can multiply each coordinate by the corresponding column of the transformation matrix to get the result:
Another example is a 90 degree rotation of space. ends up at , ends up at
We get transformation matrix:
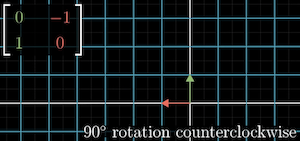
We can determine where vector lands as
Another example is a Sheer Transformation. remains fixed. moves to the coordinates
We get transformation matrix:

We can determine where vector lands as
If the columns of a transformation matrix are linearly dependent, the linear transformation "squishes" space into a single line.
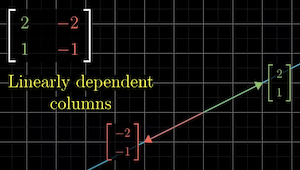
The span of those 2 vectors is 1-dimensional in this case.