Linear Transformations and Matrices

Oct 26, 2021 ../essence-of-linear-algebra

Notes from Linear transformations and matrices by 3Blue1Brown from the Essence of linear algebra series

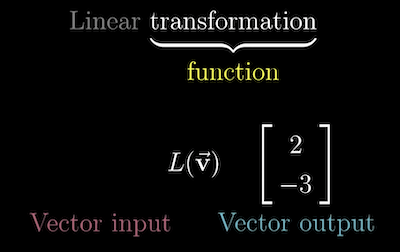
Breaking down "Linear Transformation":

  • Transform: another name for a function, in that it takes an input and returns the output.
  • However, a "transformation" implies the ability to move the transformation as "movement".
  • Linear: limits the types of transformation to ones that have these visual properties:
    • All lines, remain lines.
    • Origin remains fixed in place.
  • This keeps the grid lines parallel and evenly spaced.

To record a transformation numerically, you only need to store where the Basis Vectors, i^\hat{i} and j^\hat{j} land.

Consider vector v⃗=[−12]\vec{v} = \begin{bmatrix}-1 \\ 2\end{bmatrix}

We know it's just a linear combination of i^\hat{i} and j^\hat{j}: v⃗=−1i^+2j^\vec{v} = -1\hat{i} + 2\hat{j}

We know grid lines become evenly spaced.

So, after applying the transformation, the property: v⃗=−1i^+2j^\vec{v} = -1\hat{i} + 2\hat{j} still applies, it's just the basis vectors that have been transformed.

That means we can fully describe a 2d transformation with four numbers (2 vectors).

We put these numbers into a 2x2 matrix, called a Matrix Transformation. Each column is one of the transformed Basis VectorsTransformation matrix

So for any vector, we can multiply each coordinate by the corresponding column of the transformation matrix to get the result:

[32−21][57]=5[3−2]+7[21]\begin{bmatrix}3 && 2 \\ -2 && 1\end{bmatrix} \begin{bmatrix}5 \\ 7\end{bmatrix} = 5\begin{bmatrix}3 \\ -2\end{bmatrix} + 7\begin{bmatrix}2 \\ 1\end{bmatrix}

Another example is a 90 degree rotation of space. i^\hat{i} ends up at [01]\begin{bmatrix}0 \\ 1\end{bmatrix}, j^\hat{j} ends up at [−10]\begin{bmatrix}-1 \\ 0\end{bmatrix}

We get transformation matrix: [0−110]\begin{bmatrix}0 && -1 \\ 1 && 0\end{bmatrix}

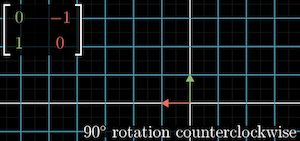
90 degree rotation

We can determine where vector u⃗=[ab]\vec{u} = \begin{bmatrix}a \\ b\end{bmatrix} lands as a[01]+b[−11]a\begin{bmatrix}0 \\ 1\end{bmatrix} + b\begin{bmatrix}-1 \\ 1\end{bmatrix}

Another example is a Sheer Transformation. i^\hat{i} remains fixed. j^\hat{j} moves to the coordinates [11]\begin{bmatrix}1 \\ 1\end{bmatrix}

We get transformation matrix: [1101]\begin{bmatrix}1 && 1 \\ 0 && 1\end{bmatrix}

Shear transformation

We can determine where vector u⃗=[ab]\vec{u} = \begin{bmatrix}a \\ b\end{bmatrix} lands as a[10]+b[11]a\begin{bmatrix}1 \\ 0\end{bmatrix} + b\begin{bmatrix}1 \\ 1\end{bmatrix}

If the columns of a transformation matrix are linearly dependent, the linear transformation "squishes" space into a single line.

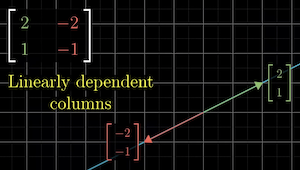
Linear dependent columns

The span of those 2 vectors is 1-dimensional in this case.