Matrix Inverse
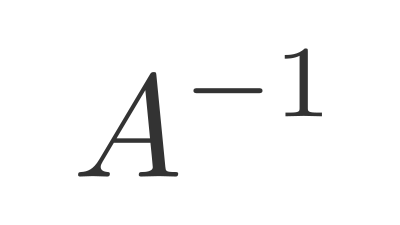
The inverse of a Matrix Transformation is a matrix that reverses the transformation.
For example, if our matrix transform did a 90° anticlockwise rotation, the inverse matrix would do a 90° clockwise rotation.
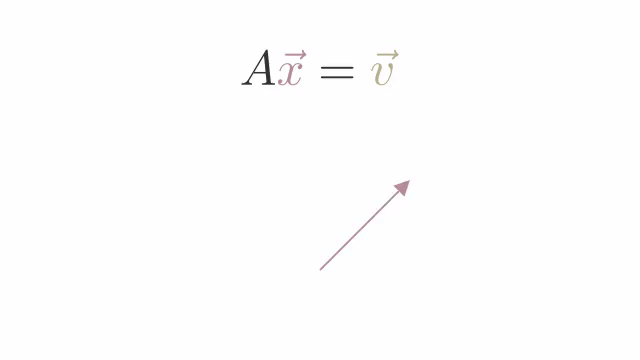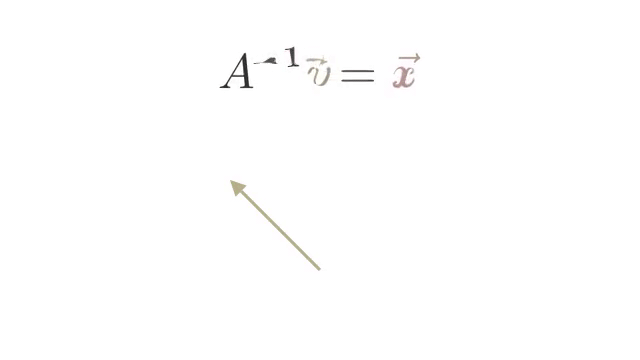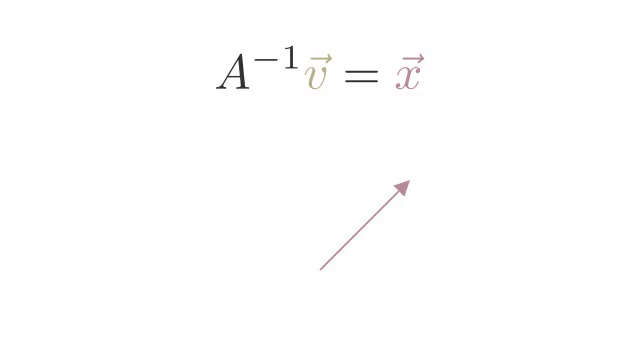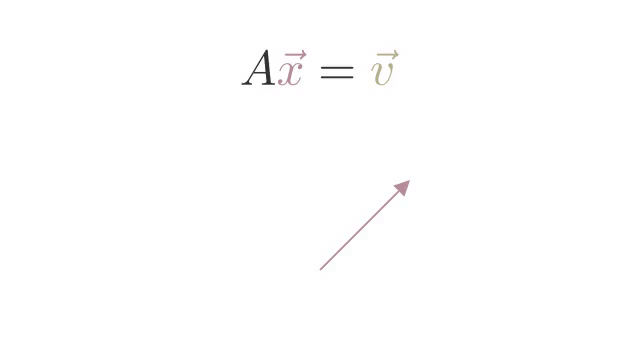
We represent the inverse of a matrix as .
When you multiply a matrix by its inverse, you get the Identity Matrix back:
It's the equivalent of the reciprocal of a number in scalar math, ie or
For a matrix, we calculate the inverse as follows:
For example:
We can do a matrix multiplication to confirm the identity matrix is returned:
We can also use the np.linalg.inv method in Numpy to find the inverse.
import numpy as np
m = np.array([[1, 3], [2, 4]])
m_inv = np.linalg.inv(m); m_inv
array([[-2. , 1.5],
[ 1. , -0.5]])
m @ m_inv
array([[1., 0.],
[0., 1.]])
The part of the expression is the Matrix Determinate.
For a larger matrix, we can use Gaussian Elimination to invert a matrix.
A matrix with a determinate of 0: is referred to as a Singular Matrix and has no inverse.
We can only calculate the inverse of a square matrix.
References
David Dye, Sam Cooper, and Freddie Page. Mathematics for Machine Learning: Linear Algebra - Home. 2018. URL: https://www.coursera.org/learn/linear-algebra-machine-learning/home/welcome. ↩
Khan Academy Labs. Introduction to matrix inverses. June 2008. URL: https://www.khanacademy.org/math/algebra-home/alg-matrices#alg-intro-to-matrix-inverses. ↩