Negative Log-Likelihood

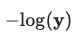
a multi-class classification loss function

Lex Toumbourou · Jul 10, 2021

Negative log-likelihood, or NLL, is a Loss Function used in multi-class classification. It measures how closely our model predictions align with the ground truth labels.

It is calculated as $-log(\hat{y})$ , where $\hat{y}$ is the prediction corresponding to the true class label after the model outputs are converted into probabilities by applying the Softmax Function to them. The loss for a mini-batch is computed by calculating the NLL for each item and then calculating the mean or sum of all items in the batch.

Since a negative value is returned for the log of a number greater than 0 and less than 1, we add a negative sign to convert it to a positive number, hence negative log-likelihood. At 0 the function returns $\infty$ ( $-log(0)=\infty$ ) and at 1 returns 0 ( $-log(1)=0$ ), so very wrong answers are heavily penalised.

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0.01, 1.0, 0.001)
y = -np.log(x)

fig,ax = plt.subplots(figsize=(6,4))
ax.plot(x,y)
plt.ylabel('-log(x)')
plt.xlabel('x')
plt.title('Negative log-likelihood range')
plt.show()

Line plot of -log(x) for x from 0.01 to 1: the value is about 4.6 near 0, falls steeply, and reaches 0 at x = 1.

Because the Softmax Function tends to force a single significant number, the loss function only needs to be concerned with the loss corresponding to the correct labels.

In PyTorch, the function is called torch.functional.nll_loss, although it doesn't take the log, as it expects outputs from a LogSoftmax activation layer.

Referred to as Log Loss in binary classification problems.

Code example:

import numpy as np, pandas as pd
from torch import tensor, nn

def softmax(x):
    return np.exp(x) / np.exp(x).sum(axis=1, keepdims=True)

labels = [0, 2, 1, 3]
logits =  np.array([
    [3.5, -3.45, 0.23, 1.25],
    [-2.14, 0.54, 2.67, -5.23],
    [-1.34, 5.01, -1.54, -1.17],
    [ -2.98, -1.37, 1.54,5.23]
])
probs = softmax(logits)
log_probs = np.log(softmax(logits))

nll = -(log_probs[range(len(labels)), labels])
nll

array([0.13484927, 0.11987498, 0.00523357, 0.02625655])

We can check to see that is equal to the output of NLLLoss, with no mean or sum reduction step.

nn.NLLLoss(reduction='none')(tensor(log_probs), tensor(labels))

tensor([0.1348, 0.1199, 0.0052, 0.0263], dtype=torch.float64)

Below the cell is highlighted that corresponds to the correct label.

def style_specific_cell(x):
    return ['background-color:#ccc' if i == x.label else '' for i in range(len(x))]

df = pd.DataFrame(probs, columns=['man', 'woman', 'camera', 'tv'])
df['label'] = labels
df['-log(pred)'] = nll


df.style.apply(style_specific_cell, axis=1)

	man	woman	camera	tv	label	-log(pred)
0	0.873848	0.000838	0.033212	0.092103	0	0.134849
1	0.007227	0.105412	0.887031	0.000329	2	0.119875
2	0.001738	0.994780	0.001423	0.002060	1	0.005234
3	0.000265	0.001325	0.024325	0.974085	3	0.026257

Negative Log-Likelihood is the 2nd part of the Categorical Cross-Entropy Loss.

Negative Log-Likelihood

Recommended Reading