Notes by Lex

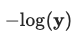
Negative log-likelihood is a loss function used in multi-class classification.

Calculated as $-log(\textbf{y})$, where $\textbf{y}$ is a prediction corresponding to the true label, after the Softmax Activation Functionon.md) was applied. The loss for a mini-batch is computed by taking the mean or sum of all items in the batch.

Since a negative value is returned for the log of a number >= 0 and < 1, we add an additional negative sign to convert to a positive number, hence negative log-likelihood. At 0 the function returns $\infty$ ($-log(0)=\infty$) and at 1 returns 0 ($-log(1)=0$), so very wrong answers are heavily penalised.

In [15]:

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0.01, 1.0, 0.001)
y = -np.log(x)

fig,ax = plt.subplots(figsize=(6,4))
ax.plot(x,y)
plt.ylabel('-log(x)')
plt.xlabel('x')
plt.title('Negative log-likelihood range')
plt.show()

BecausSoftmax Activation Functionfunction.md) tends to force a single significant number, the loss function only needs to be concerned with the loss corresponding to the correct labels.

In PyTorch, the function is called torch.functional.nll_loss, although it doesn't take the log, as it expects outputs from a LogSoftmax activation layer.

Howard et al. (2020) (pg. 226-231)

Code example:

import numpy as np, pandas as pd
from torch import tensor, nn

def softmax(x):
    return np.exp(x) / np.exp(x).sum(axis=1, keepdims=True)

labels = [0, 2, 1, 3]
logits =  np.array([
    [3.5, -3.45, 0.23, 1.25],
    [-2.14, 0.54, 2.67, -5.23],
    [-1.34, 5.01, -1.54, -1.17],
    [ -2.98, -1.37, 1.54,5.23]
])
probs = softmax(logits)
log_probs = np.log(softmax(logits))

nll = -(log_probs[range(len(labels)), labels])
nll

array([0.13484927, 0.11987498, 0.00523357, 0.02625655])

nn.NLLLoss(reduction='none')(tensor(log_probs), tensor(labels))

tensor([0.1348, 0.1199, 0.0052, 0.0263], dtype=torch.float64)

def style_specific_cell(x):
    return ['background-color:#ccc' if i == x.label else '' for i in range(len(x))]

df = pd.DataFrame(probs, columns=['man', 'woman', 'camera', 'tv'])
df['label'] = labels
df['-log(pred)'] = nll


df.style.apply(style_specific_cell, axis=1)

Negative Log-Likelihood is the 2nd part of the Categorical Cross-Entropy Loss.

Backlinks

• Categorical Cross-Entropy Loss