Notes by Lex Toumbourou

These are notes from Inverse matrices, column space, and null space video by 3Blue1Brown.

The video provides a view of Matrix Inverse and Column Space through the lens of linear transformations.

It's focused on intuition and therefore doesn't cover their computation: there are plenty of resources for that online.

One major use case for linear algebra is solving linear systems of equations.

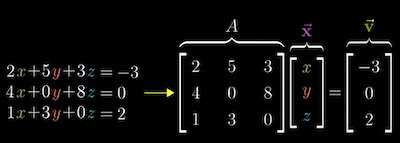
One example:

\begin{gather} 2x + 5y + 3z = -3 \\ 4x + 0y + 8z = 0 \\ 1x + 3y + 0z = 2 \\ \end{gather}

In them, we scale each variable by some value and add together each component. We organize by putting variables on the left and answers on the right. If a term isn't present, we add a 0 before the corresponding variable so everything lines up.

Can put the same information into a Matrix Multiplication

$\begin{bmatrix}2 && 5 && 3 \\ 4 && 0 && 8 \\ 1 && 3 && 0\end{bmatrix} \begin{bmatrix}x \\ y \\ z\end{bmatrix} = \begin{bmatrix}-3 \\ 0 \\ 2\end{bmatrix}$

We can visualize a Matrix Transformation geometrically by finding a vector $\vec{x}$ that, when transformed by $A$, lands on $\vec{v}$.

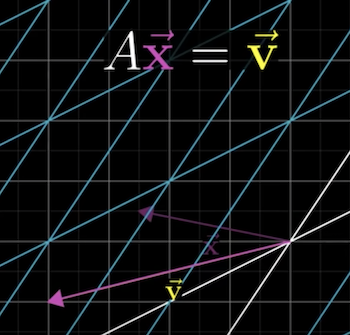
In 2d example, with 2 equations and 2 unknowns:

\begin{gather} 2x + 3y = -4 \\ 1x + 3y = -1 \end{gather}

$\underbrace{\begin{bmatrix}2 & 2 \\ 1 & 3\end{bmatrix}}_A \underbrace{\begin{bmatrix}x \\ y\end{bmatrix}}_{\vec{x}} = \underbrace{\begin{bmatrix}-4 \\ -1\end{bmatrix}}_{\vec{v}}$

An important distinction is whether the transformation squishes space onto a single line (has a Matrix Determinate of 0) or keeps things in 2d.

In the case, $\det \ne 0$, if you reversed the transformation that led to $\vec{v}$, you end up with $\vec{x}$. We can record the reverse transformation in a matrix that we call Matrix Inverse of $A$, represented as $A^{-1}$.

If $A$ is a counter-clockwise rotation $\begin{bmatrix}0 && -1 \\ 1 && 1\end{bmatrix}$, then the inverse is a clockwise rotation $\begin{bmatrix}0 && 1 \\ -1 && 0\end{bmatrix}$

If $A$ is a rightward shear that pushes space to the right $\begin{bmatrix}1 && 1 \\ 0 && 1\end{bmatrix}$ then the inverse is a leftward shear $\begin{bmatrix}1 && -1 \\ 0 && 1\end{bmatrix}$.

The core property of the inverse is that when multipled by the original matrix, the Identity Matrix is returned: $\underbrace{A^{-1}}_{\text{Inverse}}\underbrace{A}_{\text{Transform}} = \underbrace{I}_{Identity}$

When you find the inverse, you can solve for $\vec{x}$ by multiplying it by $\vec{v}$. Algebraically it works, because you can multiply both sides by the inverse.

\begin{align} A^{-1}A\vec{x} = A^{-1}\vec{v} \\ $\vec{x} = A^{-1}\vec{v} \end{align}

For a randomly generated matrix, the determinant is likely non-zero. That corresponds to the idea that two unknowns in a linear system of equations have a unique solution.

The same intuition carries over into higher dimensions.

When the [Matrix Determinate](../../../permanent/matrix-determinate.md) is 0 - it squishes space onto a single line or a point - a [Matrix Transformation](../../../permanent/matrix-transformation.md) has no inverse: you can't un-squish a line to transform it onto a plane.

When the output of a transformation is a line, we say it has Rank of 1.

If all the vectors land on a 2d plane, the transformation Rank of 2.

"Rank" refers to the number of dimensions in the output of a transformation.

In a 2d transformation, a rank 2 means that the Matrix Determinate is non-zero, and the output spans all possible space.

For a 3d transformation, a rank 2 means that the transformation is collapsing space.

The set of all possible outputs is called Column Space of a matrix. We call it this because the columns of a matrix say where the Basis Vectors land and the Vector Span of basis vectors give all possible outputs.

So, column space is equal to the span of columns in your matrix.

And a more precise definition of rank is the number of dimensions in your column space.

When the rank is as high as possible for the dimensions of the matrix, we say it has "full rank."

The vector $\begin{bmatrix}0 \\ 0\end{bmatrix}$ will always be included in the column space since linear transformations keep the origin fixed.

For a full rank transformation, the only vector that lands at origin will be the 0 vector.

For matrices that aren't full rank, you can have many matrices that land on 0. If a 2d transformation puts vectors on a line, a line full of vectors will land on the origin.

This set of vectors that land on the origin is called the Null Space or kernel of the vectors. The space of all vectors that become null (land on 0 vectors).

With linear systems of equations $A\vec{x} = \vec{v}$ when $\vec{v}$ happens to be $\begin{bmatrix}0 \\ 0\end{bmatrix}$, the null space gives you all possible solutions to the equation.