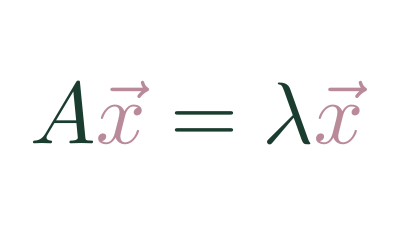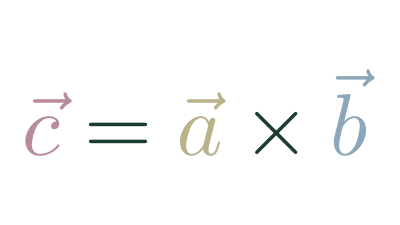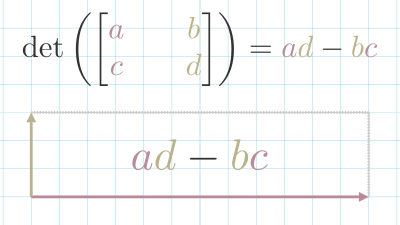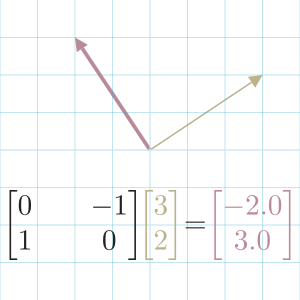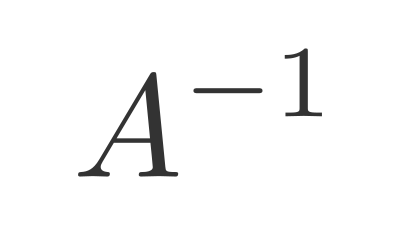Articles tagged with LinearAlgebra
-
-
-
Changing Basis
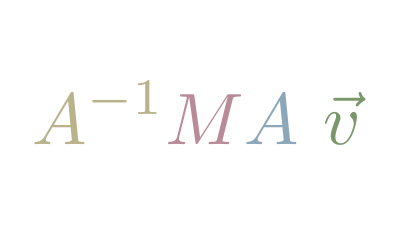
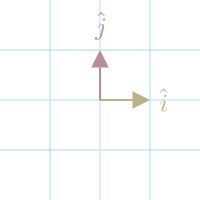
Since any vectors can be Basis Vectors, it's useful to understand how to translate vectors between bases
-
-
-
-
-
-
Identity Matrix
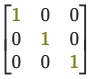
When you multiply a matrix by the Identity Matrix , you get the original matrix back.
-
Matrix Multiplication
Matrix multiplication is a mathematical operation between 2 matrices that returns a matrix.
For each row in the first matrix, take the Dot Productf …