Notes by Lex Toumbourou

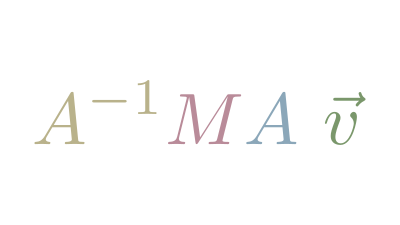
The use of coordinates to define vectors implies an agreement about which Basis Vectors we use. In 2d space, we commonly use the standard basis vectors:

$\hat{i}=\begin{bmatrix}1 \\ 0\end{bmatrix}$, $\hat{j}=\begin{bmatrix}0 \\ 1\end{bmatrix}$.

However, we are technically not limited to just the standard basis vectors: we can use any set of vectors to describe a coordinate system. Perhaps we encounter an Alien whose coordinate system uses these basis vectors:

$\hat{e}_{1} = \begin{bmatrix}2 \\ 4\end{bmatrix}$, $\hat{e}_{2} = \begin{bmatrix}1 \\ 1\end{bmatrix}$.

If the Alien describes a vector, say $\begin{bmatrix}3 \\ 1\end{bmatrix}$, in their coordinate system, we'd have first to translate it to our system.

We can translate back into our system by creating a matrix which uses the Alien basis vectors as the columns:

$\begin{bmatrix}2 && 1 \\ 4 && 1\end{bmatrix}\begin{bmatrix}3 \\ 1\end{bmatrix} = \begin{bmatrix}7 \\ 13\end{bmatrix}$

We can think of that as a Matrix Transformation that scales basis vector $\hat{e}_1$ by $3$ and $\hat{e}_2$ by $1$.

We can convert a vector described in our coordinate system to the Alien using the Matrix Inverse of our Alien's basis vector matrix:

$\begin{bmatrix}2 && 1 \\ 4 && 1\end{bmatrix}^{-1}\begin{bmatrix}7 \\ 13\end{bmatrix} = \begin{bmatrix}3 \\ 1\end{bmatrix}$

If we wish to perform a transformation described in our Basis, for example, a rotational transformation on an alternate basis, we can follow these steps:

1. Convert the vector into our Basis by applying our friend's transformation matrix.
2. Perform the translation.
3. Convert the vector back into our friend's Basis by applying the inverse of the transformation.

In notation, if we have vector $\vec{v}$ described in our friend's Basis $A$, we can apply Matrix Transformation $M$, described in our Basis, as follows:

$A^{-1}MA \ \vec{v}$